状态压缩DP
前言
本讲讲解状压DP两题经典题目
经典例题
例题 蒙德里安的梦想
题目描述
求把
例如当
如下图所示:

输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数
当输入用例
数据范围:
输出格式
每个测试用例输出一个结果,每个结果占一行。
输入样例
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例
1
0
1
2
3
5
144
51205
题目分析
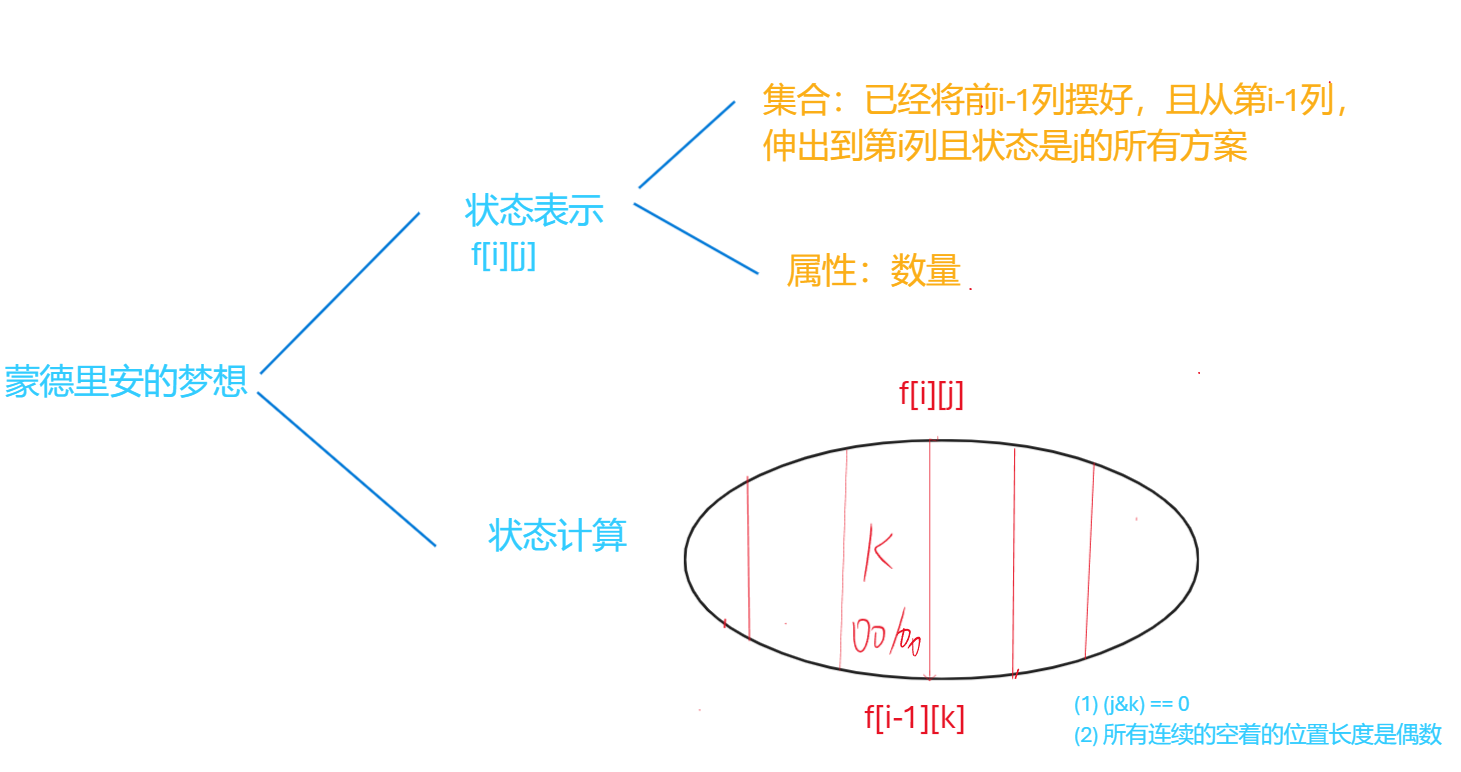
核心思想:摆放方块时,先放横着的,再放竖着的。那么总方案等于只放横着的小方块的合法方案数。
如何判断合法?因为我们找的是所有横着的方块,那么按列来看,对于每部分连续的空余的位置,必须是偶数个。
/*
下文对 if ((j & k ) == 0 && st[ j | k] ) 有清晰的解释!!!
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 12, M = 1<< N;
long long f[N][M] ;// 第一维表示列, 第二维表示所有可能的状态
bool st[M]; //存储每种状态是否有奇数个连续的0,如果奇数个0是无效状态,如果是偶数个零置为true。
//vector<int > state[M]; //二维数组记录合法的状态
vector<vector<int>> state(M); //两种写法等价:二维数组
int m, n;
int main() {
while (cin >> n >> m, n || m) { //读入n和m,并且不是两个0即合法输入就继续读入
//第一部分:预处理1
//对于每种状态,先预处理每列不能有奇数个连续的0
for(int i = 0; i < (1 << n); i ++) {
int cnt = 0 ;//记录连续的0的个数
bool isValid = true; // 某种状态没有奇数个连续的0则标记为true
for(int j = 0; j < n; j ++) { //遍历这一列,从上到下
if ( (i >> j) & 1) {
//i >> j位运算,表示i(i在此处是一种状态)的二进制数的第j位;
// &1为判断该位是否为1,如果为1进入if
if (cnt & 1) {
//这一位为1,看前面连续的0的个数,如果是奇数(cnt &1为真)则该状态不合法
isValid =false;
break;
}
cnt = 0; // 既然该位是1,并且前面不是奇数个0(经过上面的if判断),计数器清零。
//其实清不清零没有影响
}
else cnt ++; //否则的话该位还是0,则统计连续0的计数器++。
}
if (cnt & 1) isValid = false; //最下面的那一段判断一下连续的0的个数
st[i] = isValid; //状态i是否有奇数个连续的0的情况,输入到数组st中
}
//第二部分:预处理2
// 经过上面每种状态 连续0的判断,已经筛掉一些状态。
//下面来看进一步的判断:看第i-2列伸出来的和第i-1列伸出去的是否冲突
for (int j = 0; j < (1 << n); j ++) { //对于第i列的所有状态
state[j].clear(); //清空上次操作遗留的状态,防止影响本次状态。
for (int k = 0; k < (1 << n); k ++) { //对于第i-1列所有状态
if ((j & k ) == 0 && st[ j | k])
// 第i-2列伸出来的 和第i-1列伸出来的不冲突(不在同一行)
//解释一下st[j | k]
//已经知道st[]数组表示的是这一列没有连续奇数个0的情况,
//我们要考虑的是第i-1列(第i-1列是这里的主体)中从第i-2列横插过来的,
//还要考虑自己这一列(i-1列)横插到第i列的
//比如 第i-2列插过来的是k=10101,第i-1列插出去到第i列的是 j =01000,
//那么合在第i-1列,到底有多少个1呢?
//自然想到的就是这两个操作共同的结果:两个状态或。 j | k = 01000 | 10101 = 11101
//这个 j|k 就是当前 第i-1列的到底有几个1,即哪几行是横着放格子的
state[j].push_back(k);
//二维数组state[j]表示第j行,
//j表示 第i列“真正”可行的状态,
//如果第i-1列的状态k和j不冲突则压入state数组中的第j行。
//“真正”可行是指:既没有前后两列伸进伸出的冲突;又没有连续奇数个0。
}
}
//第三部分:dp开始
memset(f, 0, sizeof f);
//全部初始化为0,因为是连续读入,这里是一个清空操作。
//类似上面的state[j].clear()
f[0][0] = 1 ;// 这里需要回忆状态表示的定义
//按定义这里是:前第-1列都摆好,且从-1列到第0列伸出来的状态为0的方案数。
//首先,这里没有-1列,最少也是0列。
//其次,没有伸出来,即没有横着摆的。即这里第0列只有竖着摆这1种状态。
for (int i = 1; i <= m; i ++) { //遍历每一列:第i列合法范围是(0~m-1列)
for (int j = 0; j < (1<<n); j ++) { //遍历当前列(第i列)所有状态j
for (auto k : state[j]) // 遍历第i-1列的状态k,如果“真正”可行,就转移
f[i][j] += f[i-1][k]; // 当前列的方案数就等于之前的第i-1列所有状态k的累加。
}
}
//最后答案是什么呢?
//f[m][0]表示 前m-1列都处理完,并且第m-1列没有伸出来的所有方案数。
//即整个棋盘处理完的方案数
cout << f[m][0] << endl;
}
}
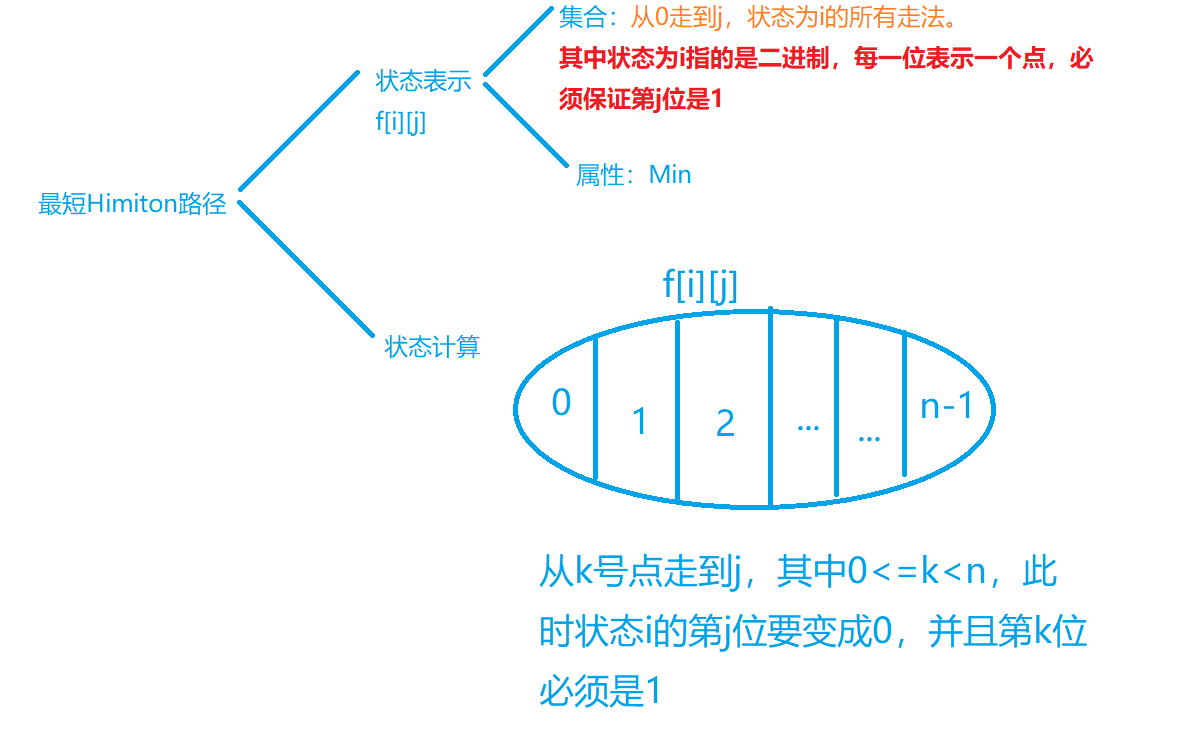
习题 最短Hamilton路径 J31802
给定一张
Hamilton 路径的定义是从
输入格式
第一行输入整数
接下来
对于任意的
数据范围:
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
输入样例
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例
18
示例代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1 << 20, M = 30;
int f[N][M], w[M][M];
int main()
{
int n;
cin >> n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
cin >> w[i][j];
memset(f, 0x3f, sizeof(f));
f[1][0] = 0; //初始化,走到0号点的代价是0
for(int i = 0; i < 1 << n; i++) //枚举所有的状态
for(int j = 0; j < n; j++) //枚举所有的点
if((i >> j) & 1) //如果状态i的第j位是1,那么可以走
{
//状态转移,从第k个走到第j个
for(int k = 0; k < n; k++)
//i的第j位变成0,且第k位是1
if((i ^ (1 << j)) >> k & 1)
f[i][j]=min(f[i][j], f[i^(1<<j)][k] + w[k][j]);
}
cout << f[(1 << n) - 1][n - 1];
return 0;
}