背包问题
本讲前言
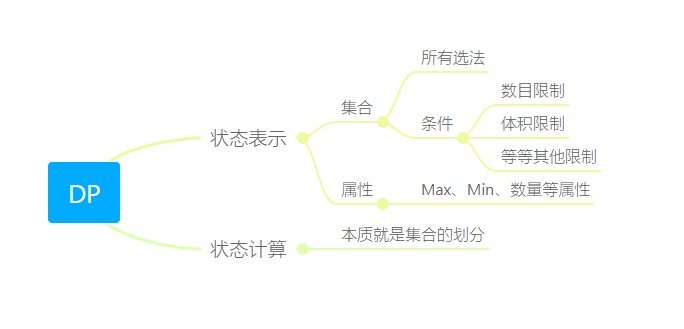
对于任何一题 DP 题,我们都可以按照以上方法去思考,对于状态计算中集合的划分,遵循以下原则:
-
不重不漏,不重有特例,有些时候可以重复。
-
将集合划分为更小的子集,假设之前的状态已经算出,推导所有子集。
-
初始状态必须明确
目前考试很注重DP的优化,优化无非就是对集合的划分的优化,通俗点说,就是对状态转移的优化。
在分析一题DP题的时候,我们先考虑如何来表示状态,一般情况下可以从题目、过往经验入手,即题目是一道DP裸题,或者是我们学过的某种DP的变形,一般情况下都是后者,这时我们对于状态表示中的集合就可以通过已有模型去替换。这是非常重要的一点,因为我们去思考DP题目的时候,如果不通过已有模型进一步思考,就会比较难想到表示方法。
我们在现阶段主要学习背包问题、最长上升子序列、线性DP、区间DP、计数类DP、数位统计DP、状压DP以及树形DP的经典模型题。以充足“储备”。
所以现阶段目标是把十八题例题完全吃透、弄懂。
之后的学习中(四阶段),我们再继续深入的剖析动态规划。
经典例题
例题 01背包问题 J31501
问题描述
有
第
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。
输入格式
第一行两个整数,
接下来有
数据范围:
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
题目分析
01背包问题是比较简单的动态规划问题,也是其余背包问题的基础,基本上所有的背包问题都是从01背包发展而来,所以弄懂01背包问题既是学习背包问题的基础,也是重点。
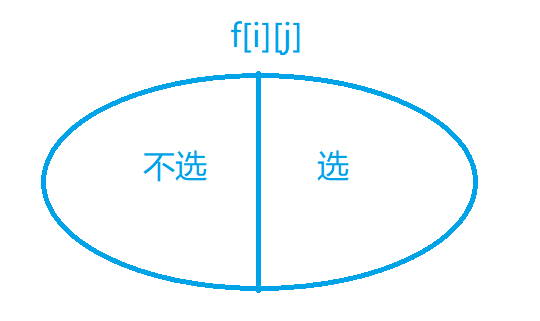
这里略微思考下暴力的做法:每个物品都有选和不选两种决策,
我们都知道,动态规划是不断决策去求最优解的过程,01背包即是不断对第
由此我们可以推断出: 状态表示:
-
集合:只从前
个物品中选,体积不超过j的所有选法的集合。 -
属性:最大值。
状态计算:
-
不选第i个物品:意味着
,此公式的含义是,不选第 个物品,那么从前 个物品中选体积不超过 的最大值。 -
选第
个物品:意味着 ,此公式的含义是,选第 个物品,那么在选好了前 个物品的情况下,留出 的空间(即 )给 物品,再加上第 个物品的价值 即可。 -
那么选和不选中选择最大值就是我们
的值,统一后公式为: -
初始状态:
,即体积为0时,不管选什么物品,最大价值都为0。

示例代码一
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N][N], v[N], w[N];
int n, m;
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++) {
f[i][j] = f[i-1][j]; //不选
if(j >= v[i])
f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]); //选
}
cout << f[n][m];
return 0;
}
优化空间:
通过代码我们发现,
其实是不需要的,因为
示例代码二
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N], v, w;
int n, m;
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> v >> w;
for(int j = m; j >= v; j--) {
f[j] = max(f[j], f[j-v] + w); //f[j-v[i]]是i-1层的
}
}
cout << f[m];
return 0;
}
代码中的
例题 完全背包问题 J31502
题目描述
有
第
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,
接下来有
数据范围:
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
题目分析
我们目前已经学习了
完全背包和
可以画个图理解一下:
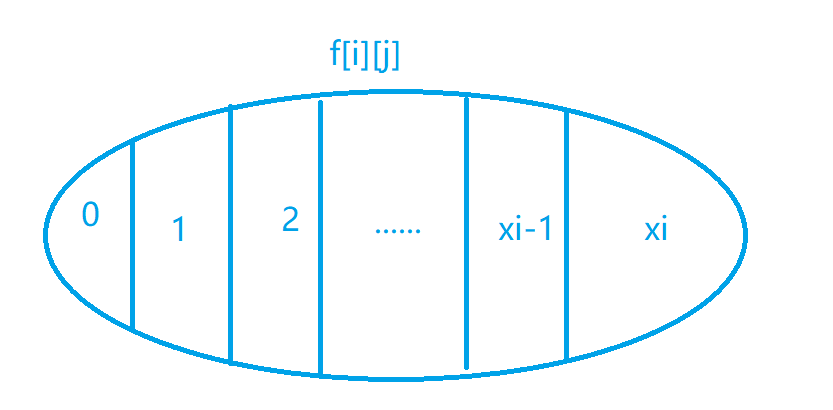
即对于前
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N], v[N], w[N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ )
for(int j = 0; j <= m; j ++ )
for(int k = 0; k * v[i] <= j; k ++ ) //k个表示物品i的个数
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);//求出每一个 f[i][j]
cout << f[n][m] << endl;
}
此代码在
但是,此代码时间复杂度为
优化过程如下:
可以发现,第二个式子相当于第一个式子除第一项之外的后面的项,只是少加了一个
那么
我们再来回忆一下
可以发现,
更通俗的理解是,我们在考虑第
综上分析,我们可以总结为:
状态表示
- 集合
- 只从前
个物品中选,体积不超过 的所有选法的集合。
- 只从前
- 属性
- 最大值。
状态计算
- 集合划分
- 选
个 - 选
个 - ...
- 选
个
- 选
- 状态转移方程
所以我们可以写出如下代码:时间复杂度
示例代码
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N], v[N], w[N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ ) {
for(int j = 0; j <= m; j ++ ) {
f[i][j] = f[i - 1][j];
if(v[i] <= j)
f[i][j] =max(f[i - 1][j], f[i][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
}
同样的,我们依旧可以变成滚动数组,和
代码如下:
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=1010;
int f[N];
int v, w;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin >> v >> w;
for(int j = v; j <= m; j++)
f[j] = max(f[j], f[j-v] + w);
}
cout << f[m] << endl;
}
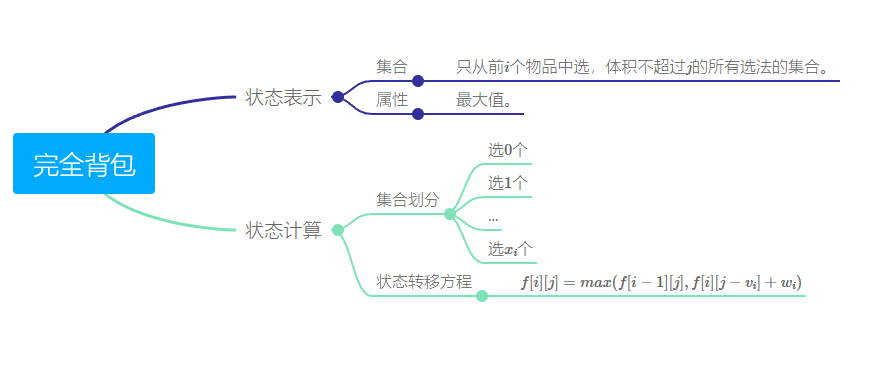
至此,我们已经分析完了完全背包问题。
分析简图如下:
例题 多重背包问题I J31503
问题描述
有
第
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,
接下来有
数据范围:
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
题目分析
本题和
代码如下:时间复杂度
/*多重背包问题1*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 + 20;
int v[N], w[N], s[N];
int n, m;
int f[N][N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= s[i] && k * v[i] <= j; k++) //直接枚举数量
f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
cout << f[n][m] << endl;
}
例题 多重背包问题II J31504
题目描述
有
第
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,
接下来有
数据范围:
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
题目分析
本题和例题三相比,数据范围更大了,同样的做法会超时,所以我们需要进行优化,这里介绍一个常见优化技巧:二进制优化。
考虑思路:对于第
示例代码
/*多重背包问题2*/
#include<bits/stdc++.h>
using namespace std;
const int N = 15000, M = 2020;
int w[N], v[N], f[M];
int n, m;
int main()
{
cin >> n >> m;
int cnt = 0;
for(int i = 0; i < n; i++)
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while(k <= s) //打包
{
cnt ++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k <<= 1;
}
if(s > 0) //如果最后还有剩余,额外打包一次,因为不能保证一定能完整打包
{
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
}
这就是多重背包的二进制优化。
当然,多重背包还有更加高效的优化方式,即单调队列优化方式,这个方法我们将在之后的学习中继续学习。
例题 分组背包问题 J31505
问题描述
有
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数
接下来有
- 每组数据第一行有一个整数
,表示第 个物品组的物品数量; - 每组数据接下来有
行,每行有两个整数 ,用空格隔开,分别表示第 个物品组的第 个物品的体积和价值;
数据范围:
输出格式
输出一个整数,表示最大价值。
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
题目分析
本题和
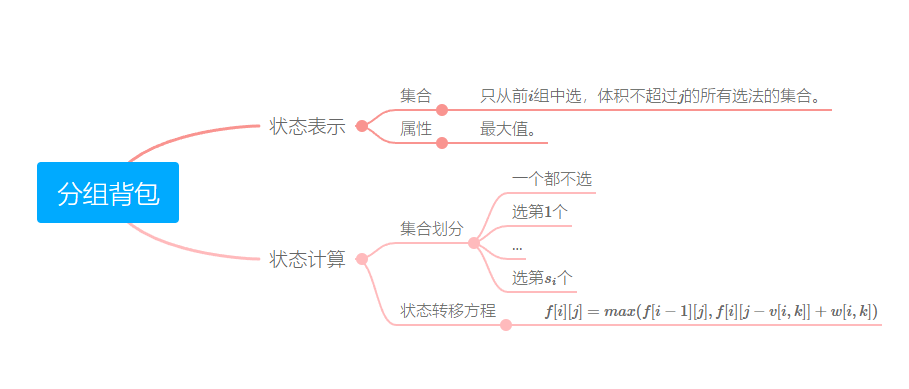
示例代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int f[N][N]; //只从前i组物品中选,当前体积小于等于j的最大值
int v[N][N], w[N][N], s[N]; //v为体积,w为价值,s代表第i组物品的个数
int n, m, k;
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int j = 0; j < s[i]; j++) {
cin >> v[i][j] >> w[i][j]; //读入
}
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j]; //不选
for (int k = 0; k < s[i]; k++) {
if (j >= v[i][k])
f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
cout << f[n][m] << endl;
}
本题也可以使用滚动数组进行优化:
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int f[N];
int w[N][N], v[N][N], s[N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> s[i];
for(int j = 0; j < s[i]; j++)
cin >> v[i][j] >> w[i][j];
}
for(int i = 1; i <= n; i++)
for(int j = m; j >= 0; j--)
for(int k = 0; k < s[i]; k++)
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m];
return 0;
}
再次深入思考一下,有没有什么办法可以继续剩下多出的二维数组的空间呢,其实可以的,我们可以边输入边处理,那么会遇到的问题有两个。
第一个问题:代码中的
由此,又会产生第二个问题:对于某一个物品,会更新掉
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int M = 110;
int f[M], last[M];
int n, m, s, v, w;
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s;
for (int j = 0; j < s; j++) {
cin >> v >> w;
for (int k = m; k >= v; k--)
f[k] = max(f[k], last[k - v] + w);
}
memcpy(last, f, sizeof f); //复制一份,保证使用第i-1层状态
}
cout << f[m] << endl;
return 0;
}
至此,空间优化成了