最短路一

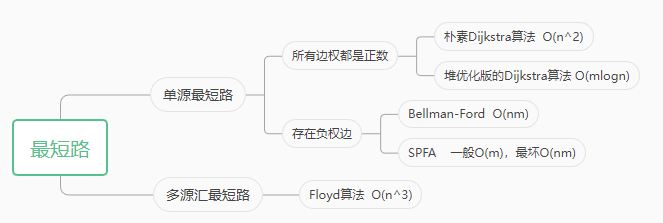
知识结构图

Pasted image 20240319162734.png

基本概念

常见的最短路问题一般可以分为两大类，单源最短路和多源汇最短路。

第一大类，单源最短路 就是求从一个点到其他点的最短距离，是最常见的。

第二大类，多源汇最短路 的问题，源就是起点的意思，汇就是终点的意思，其实就是可能不止一个起点，可能有很多询问，每个询问可能是任选几个点到其他点的距离，也就是说起点和终点都不确定的问题。

单源最短路 又能分成两种情况，一种情况是所有的边权重都是正数，图论里面有两种解决办法，都属于是 $D i j k s t r a$ 算法，但是实现的方式不同，一种是朴素 $D i j k s t r a$ 算法，另一种是堆优化版本的 $D i j k s t r a$ 算法，解决问题时要看具体情况来做选择。

我们规定 $n$ 为点的数量， $m$ 为边的数量，朴素的时间复杂度为 $O (n^{2})$ ，堆优化版本的时间复杂度为 $O ((m + n) l o g n)$ ，一般来说 $m$ 的规模不小于 $n$ 的规模，可以写为 $O (m l o g n)$ ，由此我们可以发现朴素版的时间复杂度和边是没有关系的，所以它适用于稠密图，也就是边数 $m$ 和 $n^{2}$ 是一个级别的时候，如果稠密图也用堆优化版本来做的话， $m l o g n$ 就相当于是 $n^{2} l o g n$ ，比朴素版稍微高一些，所以在这种情况下尽量选择朴素版。

如果 $m$ 和 $n$ 是一个级别的，比如说都是 $10^{5}$ 级别的，就是稀疏图，那这个时候就不能用朴素版了， $n^{2}$ 会爆掉，要用堆优化版去解决。 $n$ 和 $m$ 的数据范围在算法题目中还是比较明显的，读题的时候多注意。

另一种情况是存在负权边，也就是某些边的权重是负数，也有两种实现方式，一种是 $B e l l m a n - F o r d$ 算法，贝尔曼-福特算法，它的时间复杂度是 $O (n m)$ ，另一种是 $S P F A$ 算法，他的时间复杂度一般情况下是 $O (m)$ ，最坏情况下是 $O (n m)$ 。

总的说 $S P F A$ 算法效率是高于贝尔曼的，他是贝尔曼的一个优化，所以说大多数时候都是用 $S P F A$ 算法，但是并不是所有情况都可以用 $S P F A$ 解决，比如说经过不超过 $k$ 条边的最短路，也就是限制经过的边数小于等于 $k$ 的话，那么就用贝尔曼的方法来做比较好。

多源汇最短路 的话就是 $F l o y d$ 算法 , 它的时间复杂度是 $O (n^{3})$ 。

最短路的问题我们一定要结合实际的情况来选择对应的解决算法。主要考察的是我们能不能将题目给出的信息抽象成图的问题，建图，把它变成最短路的问题，然后就可以套用我们的思路和模版来做，所以说重点在分析问题，解决问题直接套用模版就可以了。至于具体算法为什么正确的证明大家可以课后去查一查资料，课上就不展开细讲了，因为我们图论算法侧重于实现，那么下面我们以题目的形式来看一下每一种算法的实现思路和代码模版。

例题-Dijkstra求最短路 I

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 $- 1$ 。

输入格式

第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

数据范围： $1 \leq n \leq 500$ ， $1 \leq m \leq 10^{5}$ ，图中涉及边长均不超过 $10000$ 。

输出格式

输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

如果路径不存在，则输出 $- 1$ 。

输入样例

输出样例

题目分析

读完题面最简单的想法应该是，使用搜索来寻找从起点出发所有可能到达 $n$ 点的路径，选取最短的路径作为最短路，然而我们观察数据范围，可能的路径是非常多的，时间复杂度指数级别，肯定无法在规定的时间内运行完毕，所以要用最短路算法，进一步观察所有的边权都是正数，而且观察点和边的关系，点少边多，明显是一个稠密图，所以可以使用朴素版本的 $D i j k s t r a$ 算法，时间复杂度是 $O (n^{2})$ 。

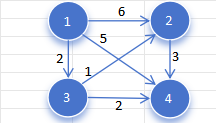
Pasted image 20240321162901.png|341

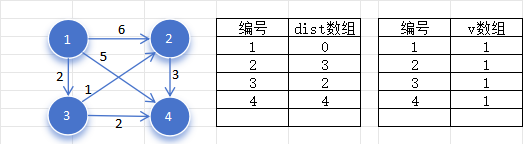
我们以上图为例，首先我们用一个 $d i s t$ 数组来记录起点到各个点的最短路长度，其中 $d i s t [i]$ 就表示从起点 $1$ 到节点 $i$ 的最短路径的长度。 $v$ 数组记录当前节点是否被标记， $v [i] = 0$ 表示节点 $i$ 未被标记， $v [i] = 1$ 表示节点 $i$ 已标记。

$D i j k s t r a$ 算法的执行的步骤如下：

初始化 $d i s t [1] = 0$ ，其余节点的 $d i s t$ 值为正无穷大，所有节点未标记，如下图：

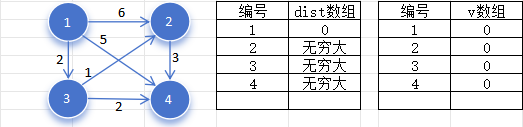
Pasted image 20240321162806.png

找出一个未被标记，并且 $d i s t [x]$ 值最小的节点 $x$ ，显然第一次找到的应该是编号为 $1$ 的节点，然后标记节点 $x$ 。如下图：

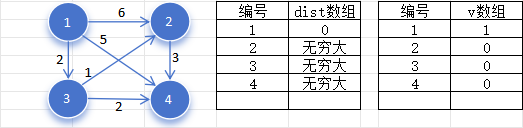
Pasted image 20240321163014.png

扫描节点 $x$ 的所有出边 $(x, y, z)$ ，若 $d i s t [y] > d i t s [x] + z$ ，则使用 $d i s t [x] + z$ 更新 $d i s t [y]$ 。显然当前节点 $1$ 有三条出边，肯定会比正无穷大要小，都满足更新条件，更新 $d i s t$ 数组，这一步叫做松弛，如下图：

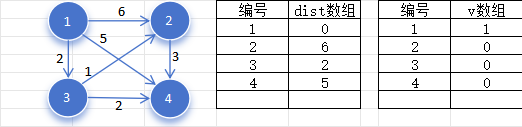
Pasted image 20240321163819.png

重复上述的2~3两个步骤，直到所有的节点都被标记。具体流程如下：
首先找到未被标记，且 $d i s t$ 值最小的点为节点 $3$ ，标记节点 $3$ 。

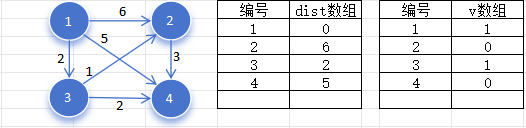
Pasted image 20240321164308.png

然后扫描节点 $3$ 的所有出边，一条是到节点 $2$ 的出边， $d i s t [2] > d i s t [3] + 1$ ，
$6 > 2 + 1$ ，所以更新 $d i s t [2] = d i s t [3] + 1$ 。一条是到节点 $4$ 的出边， $d i s t [4] > d i s t [3] + 2$ ，所以更新 $d i s t [4] = d i s t [3] + 2$ ，结果如下图：

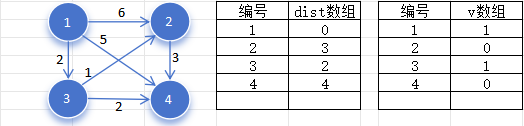
Pasted image 20240321165206.png

再次找到未被标记，且 $d i s t$ 值最小的点为节点 $2$ ，标记节点 $2$ 。

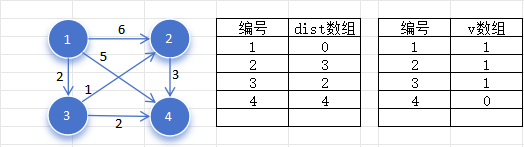
Pasted image 20240321165319.png

然后扫描节点 $2$ 的所有出边，一条是到节点 $4$ 的出边， $d i s t [4] < d i s t [2] + 3$ ，
$4 < 3 + 3$ ，所以不更新， $d i s t$ 数组不变。
再次找到未被标记，且 $d i s t$ 值最小的点为节点 $4$ ，标记节点 $4$ 。

Pasted image 20240321165629.png

然后扫描节点 $4$ 的所有出边，无出边， $d i s t$ 数组不变。到此从 $1$ 到 $n$ 的最短路就求出来了。

$D i j k s t r a$ 算法基于贪心思想，它只适用于所有边的长度都是非负数的图，当边长 $z$ 都是非负数时，全局最小值不可能再被其他节点更新，故在步骤 $2$ 中选出的节点 $x$ 必然满足： $d i s t [x]$ 已经是起点到 $x$ 的最短路径，我们不断选择全局最小值进行标记和扩展，最终可以得到起点 $1$ 到每个节点的最短路径长度，具体的贪心证明大家课后自己查阅资料，课上就不展开讲了。

示例代码

#include <bits/stdc++.h>  
using namespace std;  
int arr[1005][1005];//邻接矩阵存储每条边  
int dist[1005];//i的最短路长度  
bool v[1005];//标记数组  
int n, m, ans;  
  
int dijkstra() {  
    memset(dist, 0x3f, sizeof(dist));//dist数组初始化最大  
    memset(v, 0, sizeof(v));//节点标记  
    dist[1] = 0; //节点1  
    for (int i = 1; i < n; i++) { //重复进行n-1次 ,还有n-1个点需要标记  
        int x = -1; //寻找未标记中 dist值最小的  
        for (int j = 1 ; j <= n ; j++) {  
            if (!v[j] && (x == -1 || dist[j] < dist[x])) x = j; //未标记且最小  
        }  
        v[x] = 1; //找到后标记该节点  
        for (int y = 1; y <= n; y++) { //用当前最小值x更新其他节点  
            dist[y] = min(dist[y], dist[x] + arr[x][y]); //更新最短路  
        }  
    }  
    if (dist[n] == 0x3f3f3f3f) return -1; //未更新输出-1  
    return dist[n];  
}  
int main() {  
    scanf("%d%d", &n, &m);  
    //构建邻接矩阵  
    memset(arr, 0x3f, sizeof(arr)); //极大  
    for (int i = 1; i <= n; i++) arr[i][i] = 0;  
    for (int i = 1; i <= m; i++) { //存边  
        int x, y, z;  
        scanf("%d%d%d", &x, &y, &z);  
        arr[x][y] = min(arr[x][y], z); //有重边只保留最小边  
    }  
    ans = dijkstra();  
    printf("%d\n", ans);  
    return 0;  
}

不难看出上述代码的时间复杂度为 $O (n^{2})$ 。

例题-Dijkstra求最短路 II

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，则输出 $- 1$ 。

输入格式

第一行包含整数 $n$ 和 $m$ 。

接下来 $m$ 行每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

数据范围： $1 \leq n, m \leq 1.5 \times 10^{5}$ ，图中涉及边长均不小于 $0$ ，且不超过 $10000$ 。另外，如果最短路存在，则最短路的长度不超过 $10^{9}$ 。

输出格式

输出一个整数，表示 $1$ 号点到 $n$ 号点的最短距离。

如果路径不存在，则输出 $- 1$ 。

输入样例

输出样例

题目分析

观察这道题的 $n, m$ 数据范围不难发现这是一个稀疏图，如果还用朴素版的去解决明显不行了，观察 $n$ 的取值范围，朴素版本用邻接矩阵来存图，邻接矩阵的空间复杂度为 $O (n^{2})$ ，过大，所以需要用邻接表的来存图。

简单复习一下邻接表，我们通常使用数组模拟链表的形式实现，长度为 $n$ 的表头数组 $h e$ 记录了从每个节点出发的第一条边在 $v e r$ 和 $e d g e$ 数组中的存储位置，长度为 $m$ 的边集数组 $v e r$ 和 $e d g e$ 记录了每条边的终点和边权，长度 $m$ 的数组 $n e x t$ 模拟了链表的指针，表示从相同节点出发的下一条边在 $v e r$ 和 $e d g e$ 数组中的存储位置，如果是无向图，每加入一条边，都可以认为是加入两条相反方向的有向边，这个时候要特别注意，定义数组的元素数量上限要超过边数额两倍，邻接表的空间复杂度为 $O (n + m)$ 。

//加入有向边（x,y），权值为z
void add(int x,int y,int j){
	ver[++tot] = y,edge[tot] = z,next[tot] = head[x],head[x]=tot;
}
//访问从 x 出发的所有边
for(itn i=head[x];i;i=next[i]){
	int y = ver[i],z = edge[i];
	//找到了一条有向边(x,y), 权值为 z
}

我们再来看时间复杂度， $150000 \times 150000$ 明显过大，时间复杂度 $O (n^{2})$ 也会超时，不难发现主要的时间瓶颈在于寻找全局最小值的过程，也就是如果能很快的拿到 $d i s t$ 里面的当前未标记点的最小值，就容易了，那么我们可以用二叉堆对 $d i s t$ 数组进行维护，用 $O (l o g n)$ 的时间获取最小值并从堆中删除，用 $O (l o g n)$ 的时间执行一条边的扩展和更新，最终可在 $O (m l o g n)$ 的时间内实现 $D i j k s t r a$ 算法。

示例代码

#include <bits/stdc++.h>
using namespace std;
const int N = 150010,M = 150010;//注意该位置的变量范围定义，N点，M边
int head[N],ver[M],edge[M],ne[M],d[N];
bool v[N];
int n,m,tot,ans;
//大跟堆，pair的第二维为节点编号 
//pair的第一维为dist的相反数（利用相反数变成小根堆） 
priority_queue < pair<int,int> > q; 

void add(int x,int y,int z){
	ver[++tot] = y,edge[tot] = z,ne[tot] = head[x],head[x] = tot;
}
int dijkstra(){
	memset(d,0x3f,sizeof(d));//dist数组
	memset(v,0,sizeof(v));//节点标记 
	d[1] = 0;
	q.push(make_pair(0,1));
	while(q.size()){
		int x = q.top().second;//取出堆顶 
		q.pop(); 
		if(v[x]) continue; //确定的跳过 
		v[x] = 1;
		//扫描所有出边
		for(int i = head[x]; i ; i = ne[i]){
			int y = ver[i],z = edge[i];
			if(d[y] > d[x] + z){ //更新 把新的二元组插入堆 
				d[y] = d[x] + z;
				q.push(make_pair(-d[y],y)); 
			} 
		} 
	}
	if(d[n] == 0x3f3f3f3f) return -1;//未更新输出-1
	return d[n];
}
int main(){
	scanf("%d%d",&n,&m);
	//构建邻接表
	for(int i = 1; i <= m; i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
	} 
	ans = dijkstra();
	printf("%d",ans);
	return 0;
}

$D i j k s t r a$ 算法的优势是时间复杂度较低，缺点是一但边长出现负数其正确性就无法保证了，我们来看一道新的例题。

例题-有边数限制的最短路

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，输出 impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数 $n, m, k$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。点的编号为 $1 \sim n$ 。

$1 \leq n, k \leq 500$ , $1 \leq m \leq 10000$ , $1 \leq x, y \leq n$ , 任意边长的绝对值不超过 $10000$ 。

输出格式

输出一个整数，表示从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

输入数据

输出数据

题目分析

首先发现这道题目中的边权可能为负数， $d i j k s t r a$ 不能解决负权边是因为 $d i j k s t r a$ 要求每个点被确定后 $v [i] = t r u e$ ， $d i s t [i]$ 就是最短距离了，之后就不能再被更新了（一锤子买卖），而如果有负权边的话，那已经确定的点的 $d i s t [i]$ 不一定是最短了，就要用到我们之前提到的贝尔曼-福特算法，他的基本思路是这样的。

//首先是n次迭代
for(n){ //循环点数n
	for(所有边 x,y,z) { //从x走向y，权重是z 循环边数m
//这里注意边的存储方式不一定是邻接表，可以开结构体去存储，只要能遍历到所有边就可以了
		//和dijkstra类似，更新操作 ，叫做松弛操作
		dist[y] = min(dist[y],dist[x]+z); 
	}
}
//循环完以后 所有边xyz 一定满足 dist[y]<=dist[x]+z  这个式子三角不等式
//不难看出时间复杂度为O(nm)

但是这里要注意一个问题，如果图里面存在负权回路的话，最短路就不一定存在了有可能会在负权回路里一直转圈，结果会是负无穷，如下图：

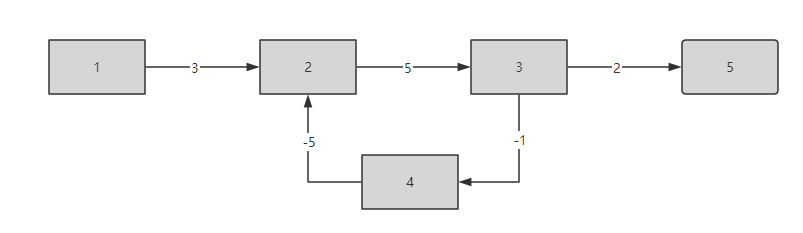
Pasted image 20240407190559.png

也就是说能求出最短路的话，一般来说图里面是没有负权回路的。贝尔曼-福特算法是可以求出来这个图是不是存在负权回路的，假如我们在外层循环迭代 $k$ 次，在内层循环求得的 $d i s t$ 数组的含义就是从 $1$ 号点出发，经过不超过 $k$ 条边，走到每个点的最短距离，也就是说迭代的时候，第 $n$ 次又更新了某条边的话，也就是说存在一条最短路径他的边数是等于 $n$ 的，那也就意味着从点 $1$ 出发到某一点 $x$ 有 $n$ 条边， $n$ 条边会有 $n + 1$ 个点那么就一定有两个点编号是一样的，那这个路径上就一定存在环，而且是更新过了之后，那么这个环就一定是负环，所以贝尔曼-福特算法是可以用来找负环的，但时间复杂度较高。

所以一般找负环是使用 $S P F A$ 算法来做的，但 $S P F A$ 算法求最短路是一定不能有负环的， $S P F A$ 算法我们后面会讲到， $S P F A$ 算法不能解决有边数限制的问题，所以这道题我们用贝尔曼-福特算法解决。那么有负权回路在什么情况下还有最短路呢？也就是说负权回路不会影响 $1$ 号点到 $n$ 号点，也就是说负权回路的点到不了 $n$ 号点，不路过他，就没影响了。

针对这道题来说限制了只能经过 $k$ 条边，所以存不存在负环都不会对结果造成影响。
下面我们来看一下 $B e l l m a n - F o r d$ 算法具体代码实现：

int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离
struct Edge{     // 边，a表示出点，b表示入点，w表示边的权重
    int x, y, z;
} edges[M];
// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford(){
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ ){
        for (int j = 0; j < m; j ++ ){
            int x = edges[j].x, y = edges[j].y, z = edges[j].z;
            if (dist[y] > dist[x] + z)
                dist[y] = dist[x] + z;
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    /*
    5号节点距离起点的距离是无穷大，5->n如果是-2，利用5号节点更新n号节点距离起点的距离，将得到10^9−2， 虽然小于10^9, 但并不存在最短路，(在边数限制在k条的条件下)。
    */
    return dist[n];
}

而且针对这道题目来说，这里面要注意边数限制为一条的情况下会出现串联的情况，举个例子如下：

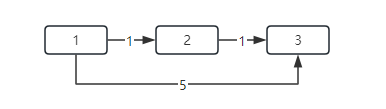
Pasted image 20240410140647.png

节点 $3$ 的距离应该是 $5$ ，但是由于串联情况，利用本轮更新的节点 $2$ 更新了节点 $3$ 的距离，所以现在节点 $3$ 的距离是 $2$ 。正确的做法是用上轮节点 $2$ 更新的距离--无穷大，来更新节点 $3$ ，再取最小值，所以节点 $3$ 离起点的距离是 $5$ 。需要定义一个 $b a c k$ 数组提前备份状态。

还有一个注意点就是源点到终点的距离正好是-1，那么 $b e l l m a n$ 会返回 -1，输出impossible。但其实正确答案是 -1。所以要在主函数去处理不存在的问题。

#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 10010;
struct Edge { //使用结构体存储边，不用定义一大堆数组去加边
    int x,y,z;
} e[M];//把每个边保存下来即可
int dist[N];
int back[N];//备份数组防止串联
int n, m, k;//k代表最短路径最多包涵k条边

void bellman_ford() {
    memset(dist, 0x3f, sizeof dist); //dist初始化位无穷，八字节3f3f3f3f大于1e9
    dist[1] = 0;
    for (int i = 0; i < k; i++) {//k次循环
        memcpy(back, dist, sizeof dist);//留存
        //遍历所有边，而dijkstra是遍历所有顶点n*n
        for (int j = 0; j < m; j++) {
            int x = e[j].x, y = e[j].y, z = e[j].z;
            dist[y] = min(dist[y], back[x] + z);
            //使用backup:避免给x更新后立马更新y
        }
    }
}
int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i++) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        e[i].x = x,e[i].y = y,e[i].z = z;
    }
    bellman_ford();
    if(dist[n]>0x3f3f3f3f/2) puts("impossible");
    else printf("%d",dist[n]);
    return 0;
}

其实同学们在做题的时候最重点的应该是如何把一个问题抽象成图的问题，然后抓住每一种算法的重点来解决问题，负环在绝大多数的题目中都是不存在的，所以接下来我们要学习的 $S P F A$ 算法，只要没有负环，它就可以使用，所以一般就是正权图 $D i j k s t r a$ 比较好用，负权图 $S P F A$ 比较好用。

先来看我们的例题。

例题-SPFA求最短路

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从 $1$ 号点到 $n$ 号点的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，输出 impossible。

注意：数据保证不存在负权回路。

输入格式

第一行包含整数 $n, m$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。点的编号为 $1 \sim n$ 。

数据范围： $1 \leq n, m \leq 10^{5}$ ，任意边长的绝对值不超过 $10000$ 。

输出格式

输出一个整数，表示从 $1$ 号点到 $n$ 号点的最短距离。

如果不存在满足条件的路径，则输出 impossible。

输入数据

输出数据

题目分析

我们学完贝尔曼-福特应该可以感觉到这个算法还是有提升的空间的，因为我们会发现它就是在傻傻的遍历点和边，全部都去看一遍，通过这个表达式 $d i s t [y] = m i n (d i s t [y], d i s t [x] + z)$ 去做松弛的操作，但是并不是每次都能成功的更新 $d i s t [y]$ ，观察这个表达式，不难发现 $d i s t [x]$ 变小了， $d i s t [y]$ 才会变小，所以我们在这里可以进行优化。

只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点，类似于广搜的思路去解决。

具体优化思路：

建立一个队列，初始时队列里只有起始点1。
再建立一个数组记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。
再建立一个数组，标记点是否在队列中。
取出队头节点 $x$ ，扫描它的所有出边 $(x, y, z)$ ，若 $d i s t [y] > d i s t [x] + z$ ，则使用 $d i s t [x] + z$ 更新 $d i s t [y]$ 。同时，若 $y$ 不在队列中，则把 $y$ 入队。
重复执行直到队列为空。
在保存最短路径的数组中，就得到了最短路径。

在任意时刻，该算法的队列都保存了待扩展的节点。每次入队相当于完成一次 $d i s t$ 数组的更新操作，使其满足三角不等式，一个节点可能会入队，出队多次。最终，图中节点收敛到全部满足三角不等式的状态，这个队列避免了 $B e l l m a n - F o r d$ 算法中对不需要扩展的节点的多余扫描，在随机图上运行效率为 $O (k m)$ 级别，其中 $k$ 是一个较小的常数，但在特殊构造的图上，类似网格图，该算法可能会退化为 $O (n m)$ ，需要特别注意。

示例代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100010,M = 100010;
int h[N],v[N],e[M],ne[M],d[N];
int n,m,tot;
queue <int> q;
int st[N];//标记 
void add(int x,int y,int z){
	v[++tot]=y,e[tot]=z,ne[tot]=h[x],h[x]=tot;
} 
void spfa(){
	memset(d,0x3f,sizeof d);
	memset(st,0,sizeof st); //是否在队列中 
	d[1]=0,st[1]=1;
	q.push(1);
	while(q.size()){
		int x = q.front();//取出队头
		q.pop();st[x]=0;//出队并取消标记
		//扫描所有的出边
		for(int i = h[x] ; i ; i = ne[i] ){
			int y = v[i] , z = e[i];
			if(d[y] > d[x]+z){
				//更新
				d[y] = d[x] + z;
				if(!st[y]) q.push(y),st[y] = 1; //入队并标记 
			}
		} 
	}
}
int main(){
	scanf("%d%d",&n,&m); 
	for(int i = 1 ;i <= m ; i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z); 
	}
	spfa();
	if(d[n] == 0x3f3f3f3f) cout <<"impossible";
	else cout << d[n];
	return 0;
}

$S P F A$ 算法看上去和 $D i j s t r a$ 算法长得有一些像但是其中的意义还是相差甚远的:

$D i j k s t r a$ 算法中的 $s t$ 数组保存的是当前确定了到源点距离最小的点，且一旦确定了最小那么就不可逆了(不可标记为 $t r u e$ 后改变为 $f a l s e$ )； $S P F A$ 算法中的 $s t$ 数组仅仅只是表示的当前发生过更新的点，且 $S P F A$ 中的 $s t$ 数组可逆(可以在标记为 $t r u e$ 之后又标记为 $f a l s e$ )。顺带一提的是 $B F S$ 中的 $s t$ 数组记录的是当前已经被遍历过的点。
$D i j k s t r a$ 算法里使用的是优先队列保存的是当前未确定最小距离的点，目的是快速的取出当前到源点距离最小的点； $S P F A$ 算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。
$B e l l m a n - f o r d$ 算法里最后的判断条件写的是 $d i s t [n] > 0 x 3 f 3 f 3 f 3 f / 2$ ;而 $S P F A$ 算法写的是 $d i s t [n] == 0 x 3 f 3 f 3 f 3 f$ ; 其原因在于 $B e l l m a n - f o r d$ 算法会遍历所有的边，因此不管是不是和源点连通的边它都会得到更新；但是 $S P F A$ 算法不一样，它相当于采用了 $B F S$ ，因此遍历到的结点都是与源点连通的，因此如果你要求的 $n$ 和源点不连通，它不会得到更新，还是保持的 $0 x 3 f 3 f 3 f 3 f$ 。

了解了 $S P F A$ 算法以后，我们来了解一下它的一个变相应用，我们来看一下下面这道例题：

例题- SPFA判断负环

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你判断图中是否存在负权回路。

输入格式

第一行包含整数 $n, m$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。点的编号为 $1 \sim n$ 。

数据范围： $1 \leq n, m \leq 10^{5}$ ，任意边长的绝对值不超过 $10000$ 。

输出格式

如果图中存在负权回路，则输出 Yes，否则输出 No。

输入数据

输出数据

题目分析

读完题目后发现其实也就是求一下图中是否存在负环的问题，基于 $S P F A$ 我们有两种求负环的方法：

统计每个点入队的次数，如果某个点入队 $n$ 次，则说明存在负环。
统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环。

一般都用方法 2，这里我们也主要讲解方法 2。

整理流程如下：

dist[x] 记录虚拟源点到n的最短距离
cnt[x] 记录当前点到虚拟源点最短路的边数，初始每个点到虚拟源点的距离为 $0$ ，只要他能再走 $n$ 步，即 cnt[x] >= n，则表示该图中一定存在负环，由于从虚拟源点到 $x$ 至少经过 $n$ 条边时，则说明图中至少有 $n + 1$ 个点，表示一定有点是重复使用。
若 dist[y] > dist[x] + z，则表示从 $x$ 点走到 $y$ 点能够让权值变少，因此进行对该点 $y$ 进行更新，并且对应 cnt[y] = cnt[x] + 1，往前走一步。

注意：该题是判断是否存在负环，并非判断是否存在从 $1$ 开始的负环，因此需要将所有的点都加入队列中，更新周围的点。

代码可以在 $S P F A$ 的基础上稍加修改得到。

示例代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100010,M = 100010;
int h[N],v[N],e[M],ne[M],d[N];
int n,m,tot;
queue <int> q;
int st[N];//标记 
int cnt[N];
void add(int x,int y,int z){
	v[++tot]=y,e[tot]=z,ne[tot]=h[x],h[x]=tot;
} 
bool spfa(){
	for(int i = 1;i<=n;i++){
		q.push(i);
		st[i] = 1;
	}
	while(q.size()){
		int x = q.front();//取出队头
		q.pop();st[x]=0;//出队并取消标记
		//扫描所有的出边
		for(int i = h[x] ; i ; i = ne[i] ){
			int y = v[i] , z = e[i];
			if(d[y] > d[x]+z){
				//更新
				d[y] = d[x] + z;
				cnt[y] = cnt[x] + 1;//如果你是较短的边那么路过的边数就是到x的边数+1 
                if (cnt[y] >= n) return true;       // 如果从1号点到x的最短路中包含至少n个点（不包括自己），则说明存在环
				if(!st[y]) q.push(y),st[y] = 1; //入队并标记 
			}
		} 
	}
	return false;
}
int main(){
	scanf("%d%d",&n,&m); 
	for(int i = 1 ;i <= m ; i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z); 
	}
	bool f = spfa();
	if(f) cout <<"Yes";
	else cout << "No";
	return 0;
}

单源最短路问题的算法就讲到这里，接下来学习最短路问题中的多源汇最短路问题，先来看例题。

例题- Floyd求最短路

题目描述

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 $k$ 个询问，每个询问包含两个整数 $x$ 和 $y$ ，表示查询从点 $x$ 到点 $y$ 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式

第一行包含三个整数 $n, m, k$ 。

接下来 $m$ 行，每行包含三个整数 $x, y, z$ ，表示存在一条从点 $x$ 到点 $y$ 的有向边，边长为 $z$ 。

接下来 $k$ 行，每行包含两个整数 $x, y$ ，表示询问点 $x$ 到点 $y$ 的最短距离。

数据范围： $1 \leq n \leq 200$ ， $1 \leq k \leq n^{2}$ ， $1 \leq m \leq 20000$ ，任意边长的绝对值不超过 $10000$ 。

输出格式

共 $k$ 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

输入数据

输出数据

impossible
1

题目分析

这道题目我们就要学习一个新的算法， $F l o y d$ 算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与 $D i j k s t r a$ 算法类似。

$F l o y d$ 属于多源最短路径算法，能够求出任意 $2$ 个顶点之间的最短路径，支持负权边，它的时间复杂度： $O (N * N * N)$ 。

实现方式是这样的，首先我们把所有的边都存在 $d [i] [j]$ 邻接矩阵中，同时引入第三个点 $k$ ，通过 $k$ 进行中转，也就是 $i \to k \to j$ ，才有可能缩短路线 $i$ 到 $j$ 的路程，举个例子如下图：

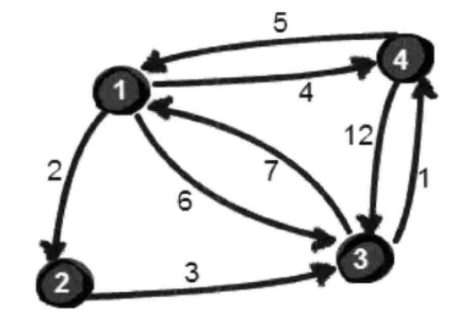
Pasted image 20240410200742.png

根据上图我们可以建立如下的邻接矩阵：

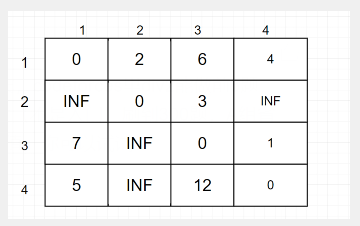
Pasted image 20240410200827.png

$4$ 号到 $3$ 号，原本 $d [4] [3] = 12$ ，通过 $1$ 中转后， $d [4] [1] + d [1] [3] = 5 + 6 = 11$ ，通过 $1$ 和 $2$ 号中转的话， $d [4] [1] + d [1] [2] + d [2] [3] = 10$ ，通过这个例子很容易得到：每个顶点都有可能使得另外两个顶点之间的路程变短。

假设我们只允许经过 $1$ 号，求任意两点之间的最短路程，应该如何求呢？只需判断 $d [i] [1] + d [1] [j]$ 是否比 $d [i] [j]$ 要小即可。由于是任意两个城市之间的最短距离，所以 $i$ 的范围是 $1 \sim n$ 同理 $j$ 也是 $1 \sim n$ 。可以写出代码如下：

for(int i=1;i<=n;++i)   //遍历起点
	for(int j=1;j<=n;++j) //遍历被缩小距离的
		if(d[i][j] > d[i][1]+d[1][j]) //如果进行中转后的距离比你现在直接到要近
			d[i][j]=d[i][1]+d[1][j];//则直接赋值给给d[i][j]即可

假设我们允许经过 $1$ 号和 $2$ 号，求任意两点之间的最短路程，应该如何求呢？
我们需要在只允许经过 $1$ 号顶点时任意两点的最短路程的结果下，再判断如果经过 $2$ 号顶点是否可以使得 $i$ 号顶点到 $j$ 号顶点之间的路程变得更短，即判断 $d [i] [2] + d [2] [j]$ 是否要比 $d [i] [j]$ 要小。

可以写出代码如下：

//经过一号顶点
for(int i=1;i<=n;++i)//遍历起点
	for(int j=1;j<=n;++j)//遍历被缩小距离的点
		//通过1号点进行中转后的距离比你现在直接到要近
		if(d[i][j] > d[i][1]+d[1][j])
			d[i][j]=d[i][1]+d[1][j];//则直接赋值给给d[i][j]即可
			
//经过二号顶点
for(int i=1;i<=n;++i)//遍历起点城市
	for(int j=1;j<=n;++j)//遍历被缩小距离的点
		//通过2号点进行中转后的距离比你现在直接到要近
		if(d[i][j] > d[i][2]+d[2][j])
			d[i][j]=d[i][2]+d[2][j];//则直接赋值给给d[i][j]即可

以此类推：当我们允许通过所有顶点中转，我们可以轻松的写出下面的算法模板。

for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
               if(d[i][j]>d[i][k]+d[k][j])
                    d[i][j]=d[i][k]+d[k][j];

重点逻辑明白了以后，这道题就不难解决了，只要注意一下实现的小细节就可以了，

示例代码

#include <bits/stdc++.h>
using namespace std;
const int N = 210, M = 2e+10, INF = 1e9;
int n, m, k, x, y, z;
int d[N][N];

void floyd() {
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i == j) d[i][j] = 0;
            else d[i][j] = INF;
    while(m--) {
        cin >> x >> y >> z;
        d[x][y] = min(d[x][y], z);
        //注意保存最小的边
    }
    floyd();
    while(k--) {
        cin >> x >> y;
        if(d[x][y] > INF/2) puts("impossible");
        //由于有负权边存在所以约大过INF/2也很合理
        else cout << d[x][y] << endl;
    }
    return 0;
}

最短路的问题同学们初学可能会觉得有一些难度，是因为最短路问题我们需要记忆的东西比较多多，这几个模版是必须要记住的，重点先把所有模版记住，弄清楚每个算法的优缺点和适用情况，灵活选择，然后难点就在我们怎么把题目抽象成图，转换成求最短路的问题。这个需要我们多做题目慢慢的去培养题目的敏感性。