深度优先搜索——DFS
基本概念
深度优先搜索可以理解为”不撞南墙不回头“,会在一条路径上一直进行搜索,直到到达这条路径的终点后,才会回头去搜索其他可能的节点,下图展示了一个可能的深度优先搜索的顺序:
数字即搜索时访问的顺序,这里设定的搜索的方案是 ”如果左边还能走,就一直往左走,否则才往右走。“
整个搜索的过程有点像——入栈和出栈,可以发现,其顺序是后进先出的,所以你想的没错,DFS的实现正是基于栈的思想。
全排列问题
来看一个问题:
例题-排列数字
题目描述
给定一个整数
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数
输出格式
按字典序输出所有排列方案,每个方案占一行。
输入样例
3
输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
题目分析
如果把
答案就是 —— 递归!
假设
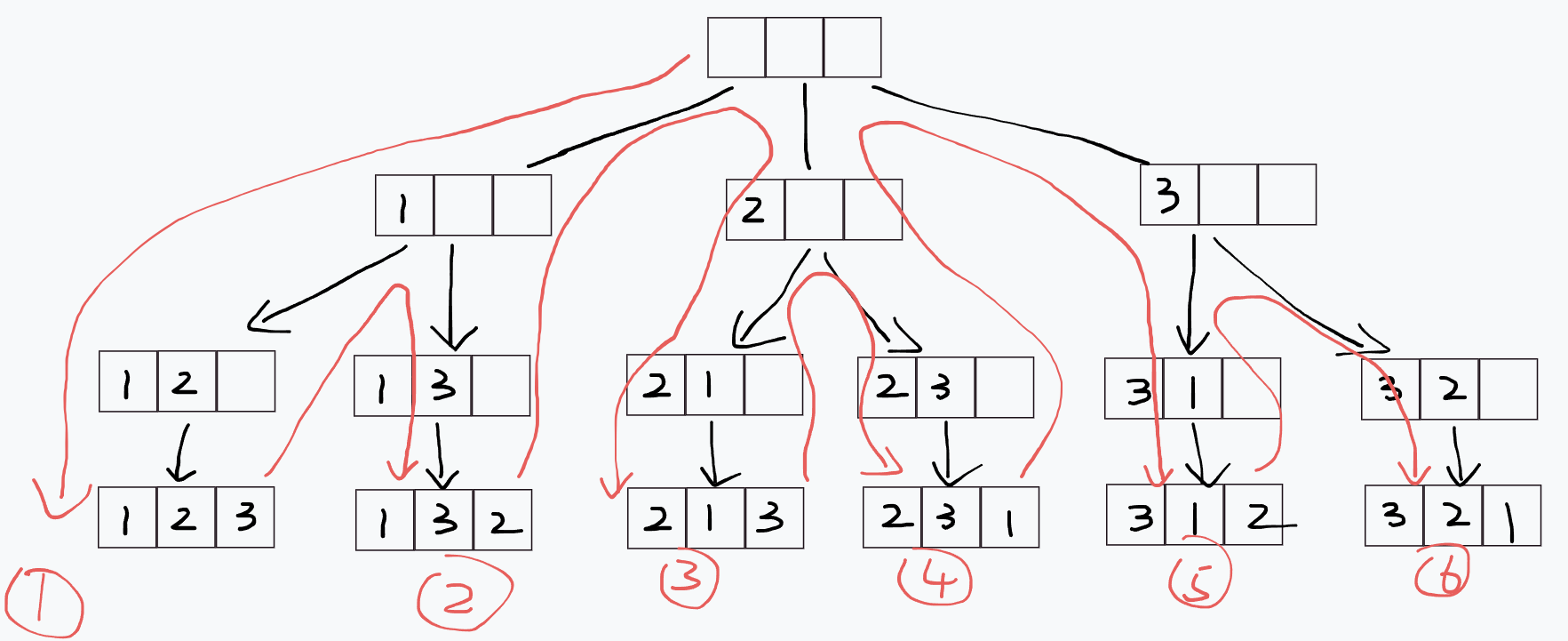
标的号是搜索的顺序。
要想实现这样的过程,需要通过哪些步骤呢?
- 其一,要往下搜索,即有一个往下递进的过程。
- 其二,要往上回溯,即有一个恢复现场的过程。
先看第一个步骤,往下递进要进行哪样的操作呢?无非就是 从
循环 1~n {
判断当前数字是否使用过: // 如何判断是否使用呢?很容易可以想到,用桶。
没有使用,选择这个数字。
标记这个数字已经使用。
递归进入下一层。
}
再看第二个步骤,回溯就是当这次调用的递归函数运行完成后,重新回到这一层时,需要”恢复成调用之前的状态“。
之前的状态是什么样的?这个数字没有被选用,所以其实就是要取消这个数字的选用,即可。
那么代码流程就变成了:
循环 1~n:
判断当前数字是否使用过: // 如何判断是否使用呢?很容易可以想到,用桶。
没有使用,选择这个数字。
标记这个数字已经使用。
递归进入下一层。
标记这个数字未使用。
取消这个数字的使用。
还剩最后一个问题,递归到什么时候结束呢?观察上面的图,我们都是走到什么地方才开始回头的?当选择了所有的数字后!所以递归的结束条件就是所有的数字都选择完!所以我们应该需要一个参数,来记录当前选择的数字的数量。
到此,递归函数的几个要素已经基本思考完成:
- 函数参数,需要一个变量
cnt来记录当前选择的数字的数量。 - 边界条件,当
cnt等于n时,表示所有数字都选了,此时终止递归函数。 - 如何进行递进,循环选择
1~n中没有被选的数字,然后递进。 - 如何进行回溯,函数调用完成后,取消数字的使用,即可完成回溯。
示例代码
#include <bits/stdc++.h>
using namespace std;
int n, vis[15];
vector<int> path;
void dfs(int cnt) {
if (cnt == n) {
// 此时说明数字全部都选了,那么应该输出答案
for (int i=0; i<n; i++) {
cout << path[i] << ' ';
}
cout << '\n';
return ;
}
for (int i=1; i<=n; i++) {
if (!vis[i]) { // 判断数字是否使用过
vis[i] = 1; // 标记数字i被使用
path.push_back(i); // 加入使用的数组中
dfs(cnt+1); // 继续往下搜索,并且使用的数字数量+1
path.pop_back(); // 已经搜索完了,将它弹出使用数组
vis[i] = 0; // 标记为未使用过
}
}
}
int main() {
cin >> n;
dfs(0);
return 0;
}
其实可以发现,这个搜索最终达到的结果,其实和枚举是很像的,都是按照某个顺序把所有可能的情况列出来,然后再根据题目的条件去进行筛选。比如,如果这一个题目加一个条件,所有选择的数字的和要刚好等于某个值,那怎么做?就在最后到达边界时加一个判断就可以了,就像在嵌套循环的最内层加一个判断一样。因此,DFS又常常被称之为暴搜,一般时间复杂度都很高,例如上面这段代码的时间复杂度介于
DFS的代码结构基本类似,如下所示:
void dfs(参数) {
if (到达边界) {
进行答案处理
return ;
}
往下递进 // 可能用循环,也可能题目的分支数是固定的,不用循环
回溯状态 // 有些情况也不用回溯
}
不过,DFS的代码并没有固定的模板,上述也只是一个常见的格式罢了,在思考相关问题时,最重要的还是思考清楚搜索的顺序、中间的限制条件、边界条件等等。
排列组合问题拓展【课后思考】
一、可重复选用的排列问题
题目描述
给定一个正整数
输入格式
共一行,包含一个整数
输出格式
按字典序输出所有排列方案,每个方案占一行。
输入样例
2
输出样例
1 1
1 2
2 1
2 2
示例代码
int n;
vector<int> path;
void dfs(int cnt) {
// cnt记录数字的数量
if (cnt == n) { // 选够n个数字了
for (int i=0; i<n; i++) cout << path[i] << ' ';
cout << '\n';
return ;
}
for (int i=1; i<=n; i++) {
// 因为可以重复选用,所以不用标记是否使用过
path.push_back(i); // 选数字
dfs(cnt+1); // 递进,注意参数范围
path.pop_back();
}
}
可以发现,和全排列问题的区别就是去掉了标记数组 vis ,时间复杂度为
二、可重复选用的组合问题
题目描述
给定两个正整数
输入格式
共一行,包含两个整数
输出格式
按字典序输出所有选择方案,每个方案占一行。
输入样例
3 5
输出样例
1 1 1 1 1
1 1 1 2
1 1 3
1 2 2
2 3
示例代码
int n, k;
vector<int> path;
void dfs(int sum, int last) {
// last在这里起到的作用
// 就是让本层的选择范围可以从上次选的数字开始,可以避免重复。
if (sum == k) { // 和为k时就是一个答案了
for (int i=0; i<path.size(); i++) cout << path[i] << ' ';
cout << '\n';
return ;
}
if (sum > k) return ; // 超过了,已经不可能是答案了
for (int i=last; i<=n; i++) {
path.push_back(i); // 选数字
dfs(sum+i, i); // 递进,注意参数范围
path.pop_back();
}
}
关键点在于每次选择数字时的范围,是 上次选的数字~n,这样做避免了枚举出重复的情况,例如枚举出 1 2 3 和 3 2 1,在这个范围下不会出现 3 2 1 ,时间复杂度为
三、不可重复选用的组合问题
题目描述
给定两个正整数
输入格式
共一行,包含两个整数
输出格式
按字典序输出所有选择方案,每个方案占一行。
输入样例
5 10
输出样例
1 2 3 4
1 4 5
2 3 5
示例代码
int n, k;
vector<int> path;
void dfs(int sum, int last) {
// last在这里起到的作用
// 就是让本层的选择范围可以从上次选的数字+1开始,可以避免重复。
if (sum == k) { // 和为k时就是一个答案了
for (int i=0; i<path.size(); i++) cout << path[i] << ' ';
cout << '\n';
return ;
}
if (sum > k) return ; // 超过了,已经不可能是答案了
for (int i=last+1; i<=n; i++) { // 注意范围,这里是last+1
path.push_back(i); // 选数字
dfs(sum+i, i); // 递进,注意传参的值
path.pop_back(); // 回溯
}
}
比起可重复的组合问题,只是范围变成了 上次选的数字+1~n ,时间复杂度为
八皇后问题
再来看一个经典问题:
八皇后问题
题目描述
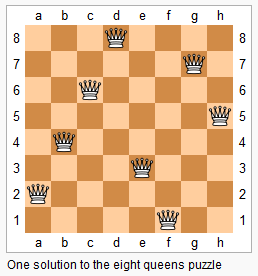
现在给定整数
输入格式
共一行,包含一个整数
输出格式
每个方案应该是一个 . 表示这个方格为空,Q 表示这个方格上摆着皇后。每输出完一个方案后,应该输出一个空行后再输出下一个方案。输出方案的顺序任意,只要不重复且没有遗漏即可。
样例输入
4
样例输出
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
第一种思路
比较容易想到一种方案,就是挨个去尝试每个格子放皇后或者不放皇后,然后最后再检查答案是否有效,可以画出其搜索树:
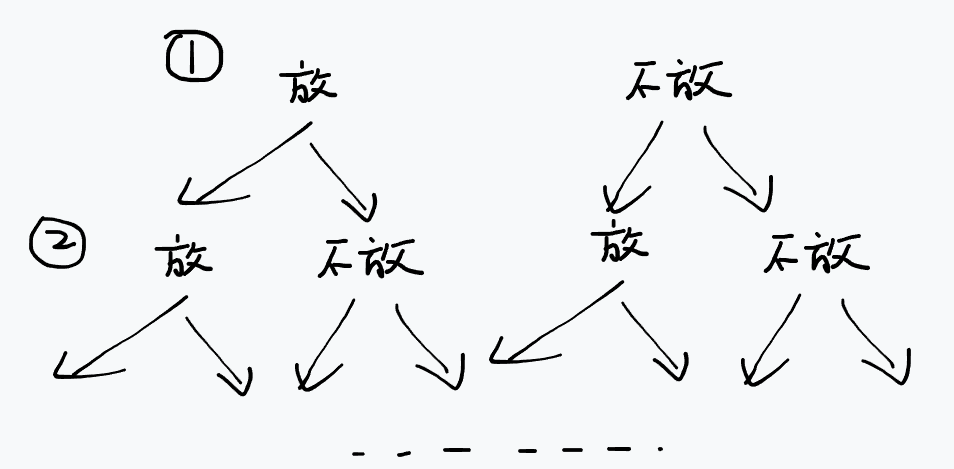
大概流程:
void dfs() {
if 到达了最后一个格子{
判断是否只有 n 个皇后,并且每个皇后之间互相不冲突。
是,则输出答案。
return ;
}
当前格子不放皇后,往下搜索;
当前格子放皇后,往下搜索;
}
其实可以发现,我们没有必要等到最后再去判断皇后之间是否冲突,在每次选择在当前格子放下皇后时,就可以判断是否有冲突,如果有冲突则直接放弃这个分支,这便是搜索中的剪枝,此案例称为可行性剪枝,即当这次搜索的结果一定不可行时,直接结束这段搜索,流程变为:
void dfs() {
if 选够了八个皇后{
输出答案。
return ;
}
if 到达了最后一个格子 {
return ;
}
当前格子不放皇后,往下搜索;
if 当前格子可以放下皇后并且不冲突 {
当前格子放皇后,往下搜索;
}
}
示例代码
int n;
int mp[25][25]; // 用来记录每个皇后是否被选用
int row[25], col[25], lf[25], rt[25];
// 行是否有皇后,列, 左对角线,右对角线
void show() {
for (int i=1; i<=n; i++) {
for (int j=1; j<=n; j++) {
if (mp[i][j]) cout << 'Q';
else cout << '.';
cout << ' ';
}
cout << '\n';
}
cout << '\n';
}
void dfs(int x, int y, int sum) {
// x表示现在在第几行,y表示现在在第几列,sum表示选择的皇后的数量
if (y == n+1) x++, y=1; // y到n+1说明这行都试完了
if (sum == n) {
show();
return ;
}
if (x == n+1) return ; // 到 n+1 说明前面的所有格子都枚举完了。
dfs(x, y+1, sum); // 不选
// 为什么对角线的下标是 x-y+n 和 x+y,可以
if (!row[x] and !col[y] and !lf[x-y+n] and !rt[x+y]) { // 四条线上都没有皇后
mp[x][y] = 1;
row[x] = col[y] = lf[x-y+n] = rt[x+y] = 1;
dfs(x, y+1, sum+1);
row[x] = col[y] = lf[x-y+n] = rt[x+y] = 0;
mp[x][y] = 0;
}
}
聪明的你应该能看出,这样每找一个格子,方案数就会翻倍,而棋盘一共有
第二种思路
再深入思考一层,其实根据题目的限制,每一行、每一列一定都只有一个皇后,那么可以利用这一特点,减少我们要搜索的东西,例如:按一行一行的顺序进行搜索,每次搜索就是尝试在当前行找一个位置放皇后,然后再去搜索下一行,这样做的好处是从搜索一格变成了搜索一行,递归最多
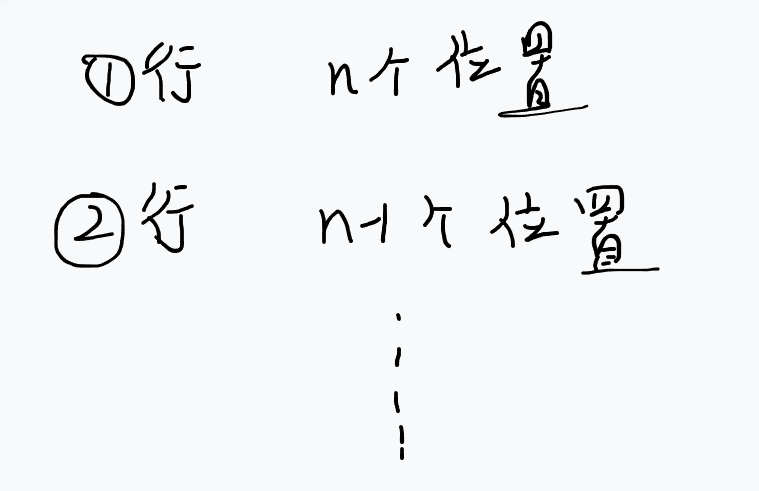
即时间复杂度上界为
void dfs() {
if 所有行都选完了{
输出答案。
return ;
}
枚举当前行的 n 个位置{
if 当前位置可以放皇后 {
放,搜索下一层;
回溯;
}
}
}
示例代码
void dfs(int x) {
// x表示现在在第几行
if (x == n+1) {
show(); // 与上面代码一致,请自行查看。
return ;
}
for (int i=1; i<=n; i++) {
if (!col[i] and !lf[x-i+n] and !rt[x+i]) { // 四条线上都没有皇后
col[i] = lf[x-i+n] = rt[x+i] = 1; // 标记有皇后了
mp[x][i] = 1; // 标记这个位置放了皇后
dfs(x+1); // 搜索下一行
mp[x][i] = 0; // 回溯
col[i] = lf[x-i+n] = rt[x+i] = 0;
}
}
}
为什么这段代码的条件不用判断行是否有冲突呢?因为搜索的顺序正是一行一行来的,所以行是一定不会有冲突的!
明显能看出,第二种方案的速度是要略快于第一种方案的,在使用DFS去解决问题时,可能会有很多种不一样的思路、想法,最重要的就是想清楚搜索的顺序。