树和图的搜索、拓扑排序
何谓树?何谓图?
树的定义
树主要解决的问题是提供一种高效、可扩展且有层次关系的数据组织方式。
其具体定义为一个有
一、每个元素称为节点(node)。
二、每个节点有零个或多个子节点。
三、没有父节点的节点称为根节点;每个非根节点有且只有一个父节点。
四、除了根节点外,每个子节点可以分为多个不相交的子树。
下图展示了一棵树的结构:
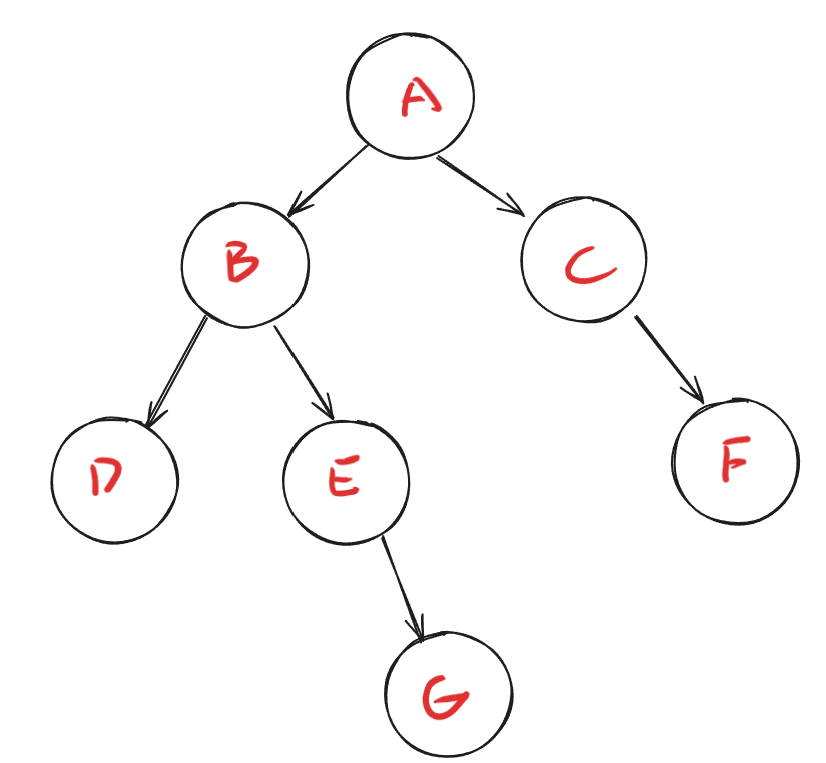
祖先:在前往某节点的路径上的所有节点,都是该节点的祖先,例如上图中,节点G的祖先有 A、B、E。
子孙:与祖先的定义相反,例如节点A的子孙有B、E、G。
父子:在上面定义的前提下,最接近的节点为父和子的关系,比如B是E的父节点,E是B的子节点。
兄弟:具有相同父节点的节点,称为兄弟,例如上图中D和E是兄弟节点。
度:一个节点的子节点的数量称为度,比如节点B的度是3。
叶子节点:度为0的节点为叶子节点。
树的深度:树中节点的最大深度,例如上图树的深度是4。
图的定义
图和树的区别在于,树的节点之间是有明显的层次关系,每个节点的上一层有且只会有一个;而图中的节点之间的关系可以是任意的,互相之间没有前后上下之分,都是同级关系。
我们在这里简单把图分成有向图和无向图。
无向图:每条边都是无方向的。
有向图:每条边都是有方向的。
完全图:任意两个点都有一条边相连。
度(无向图):与顶点相关联的边的数量。
入度(有向图):指向该顶点的边的数量。
出度(有向图):以该顶点为起点的边的数量。
权值:图中的边所具有的相关数称为权,一般表明一条边的距离或者花费。
路径:连续的边组成的顶点序列。
路径长度:路径上边的数目/权值之和。
环:第一个顶点和最后一个顶点相同的路径。
连通图:对任何两个顶点都存在路径,则称该图是连通图。
有向无环图:不存在环的有向图,简称DAG图。
稀疏图和稠密图:设图的边数为
有向图:每条边带有箭头,具有方向指向性。
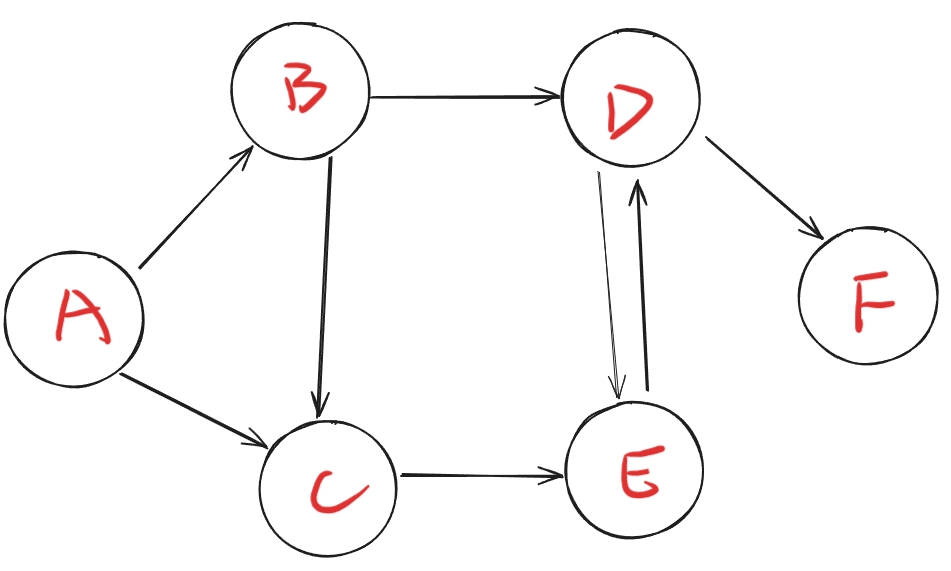
例如上图中,节点A可以前往节点C,但是节点C不能前往节点A。
无向图:每条边是不带箭头的,不具备方向指向性,可以理解为 无向图的一条边 相当于 有向图中互相连接的两条边,所以无向图可以理解为是特殊的有向图。在下图中,节点A可以前往节点C,节点C也可以前往节点A。
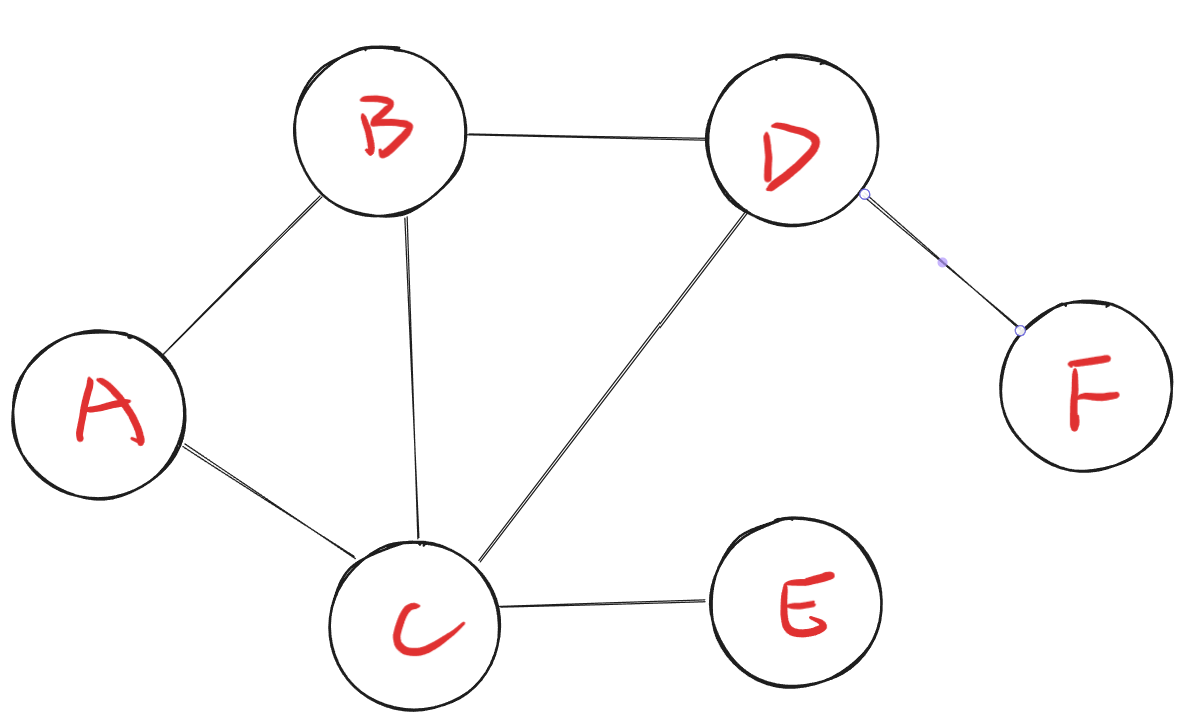
树和图的存储
回过头看看树和图的定义,无向图是特殊的有向图,而树也可以理解为是特殊的图,所以在存储方面,我们只要学习有向图的存储,就能搞定三种数据结构的存储。
一般来说,有向图的存储分为两大类,邻接矩阵和邻接表。
邻接矩阵的思想很简单,可以理解为一个二维的桶,g[a][b] 存储节点 a 到节点 b 的路径信息,其主要应用在节点和边数很接近的时候,即稠密图,当节点很多但路径很少时,邻接矩阵会比较浪费空间,下图展示了一个用邻接矩阵存储的图的结构:
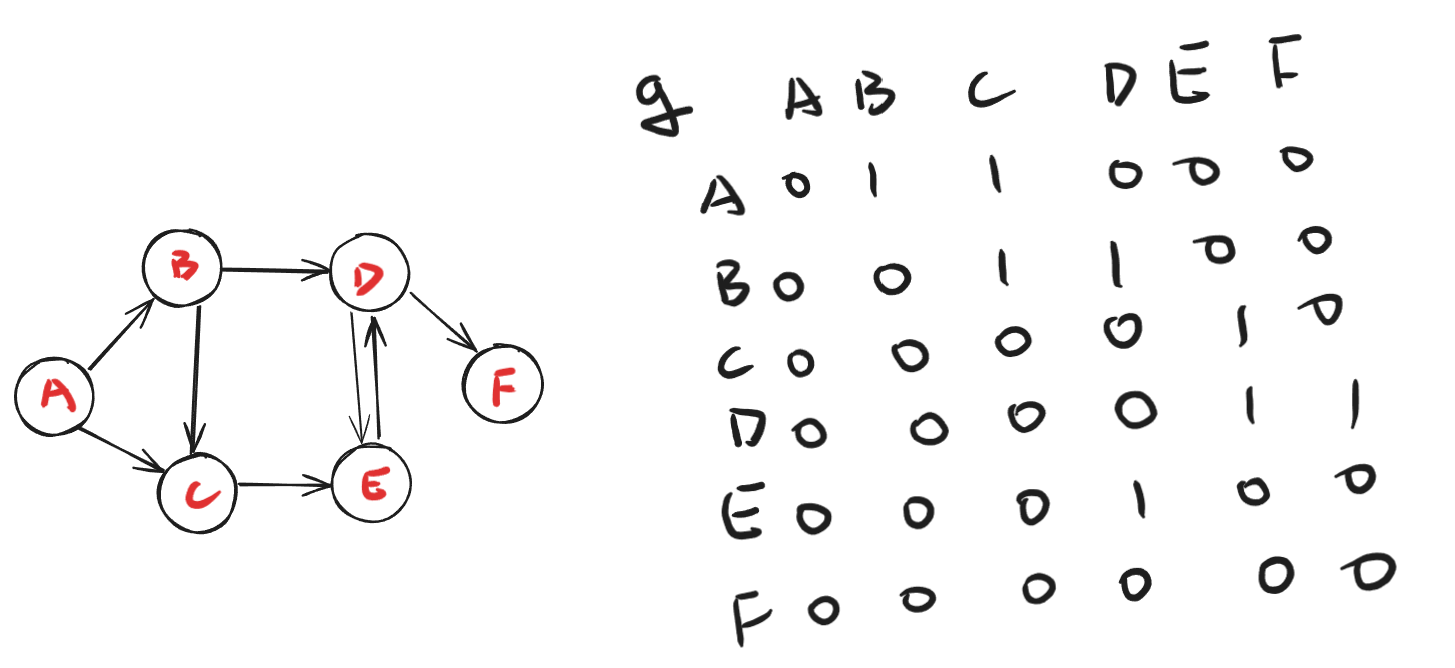
邻接表则是基于单链表的思想来实现的,每个节点都有一个自己的链表,里面存储了这个节点可以到达的所有节点以及相关的信息,下图展示了一个用邻接表存储的图的结构:
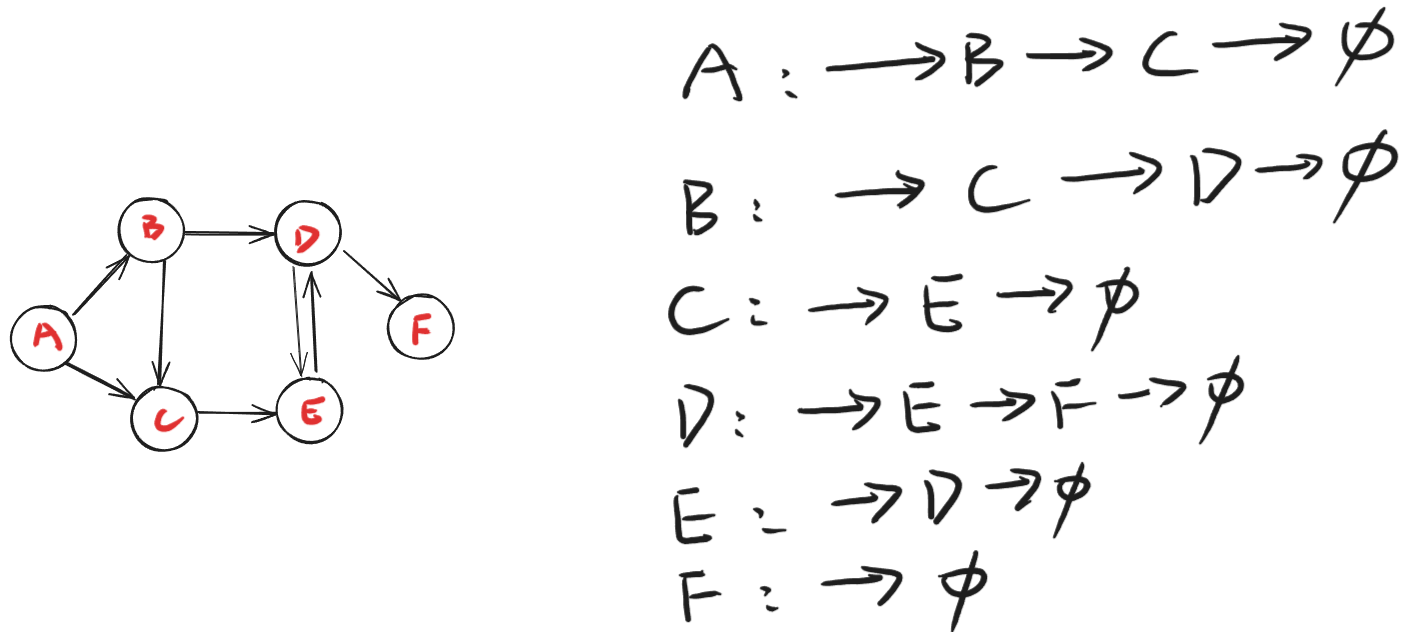
邻接表的实现和单链表其实很像,基本采取的一样是头插法,只是表头从一个变量 h 变成了一个数组 h[N],其中 h[i] 表示编号为 i 的节点对应的节点链表的头节点下标,下面展示了用邻接表实现有向图存储的代码,如下所示:
const int N = 1e5+5, M = N*2;
int h[N], e[M], ne[M], idx;
/*
h[i]: 邻接表的表头结点
e[i]:第idx条边的终点节点的信息
ne[i]:第i条边的终点节点的下一个节点
idx:表示第idx条边,也可以表示当前图中边的数量。
*/
void add(int a, int b) {
e[idx] = b; // 记录当前边的终点是b节点
ne[idx] = h[a]; // 让当前边的下一个节点指向原本的a的头节点
h[a] = idx++; // 分成两步理解,先让a的表头指向当前节点idx
// 再让idx加1,为下一次加边做准备
}
int main() {
cin >> n;
memset(h, -1, sizeof h); // 把所有点的表头都指向-1
for (int i=1; i<=n; i++) {
int a, b; // a,b表示节点a指向节点b有一条路径
cin >> a >> b;
add(a, b); // 建立一条从a指向b的路径
}
}
那么同理,如果要实现无向图,则再加一个 add(b, a) 即可,树的实现也类似。
树与图的遍历
遍历,意为从某一个节点出发,对树和图的每一个节点进行访问并且只访问一次,是求解图的连通性问题、拓扑排序等算法的基础。
DFS遍历
原理
原理很简单,从一个节点出发,然后标记这个节点已访问,并遍历该节点对应的邻接表,依次搜索该节点可以访问的所有节点,利用递归不断实现这个过程,如果这个图是一个连通图,那么必然所有节点都会被访问到,在上面邻接表的代码基础之上,实现DFS代码基础模板如下:
bool st[N]; // st[i]表示第i个点是否被访问过
void dfs(int u) {
// u表示当前所在的节点
st[u] = 1; // 标记当前节点已经访问过
cout << u << ' ';
/*
h[u]即节点u的邻接表的头节点
i!=-1是因为当i是-1时,说明后面已经没有节点了。
i = ne[i]即访问当前节点连接的下一个节点
*/
for (int i=h[u]; i!=-1; i=ne[i]) {
int j = e[i]; // 当前节点的编号
if (st[j]) continue; // 被访问过了则跳过
dfs(j); // 否则以该节点为基础继续搜索
}
}
dfs(1); // 从节点1开始搜索。
该算法的时间复杂度为
例题——树的重心
题目描述
给定一颗树,树中包含 nnn 个结点(编号
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数
接下来
输出格式
输出一个整数
样例输入
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
样例输出
4
题目分析
容易想到一个很简单的思路,就是把所有的节点都枚举一遍,计算一下当把这个节点删除时,所得到的所有联通块中的节点数的最大值是多少,然后取其中的最小值即可。
对于每个节点,被删除后剩下的连通块由以下几部分组成:
- 节点的每棵子树是一个连通块
- 除去以4为根节点的树之外,其他节点为一个连通块。
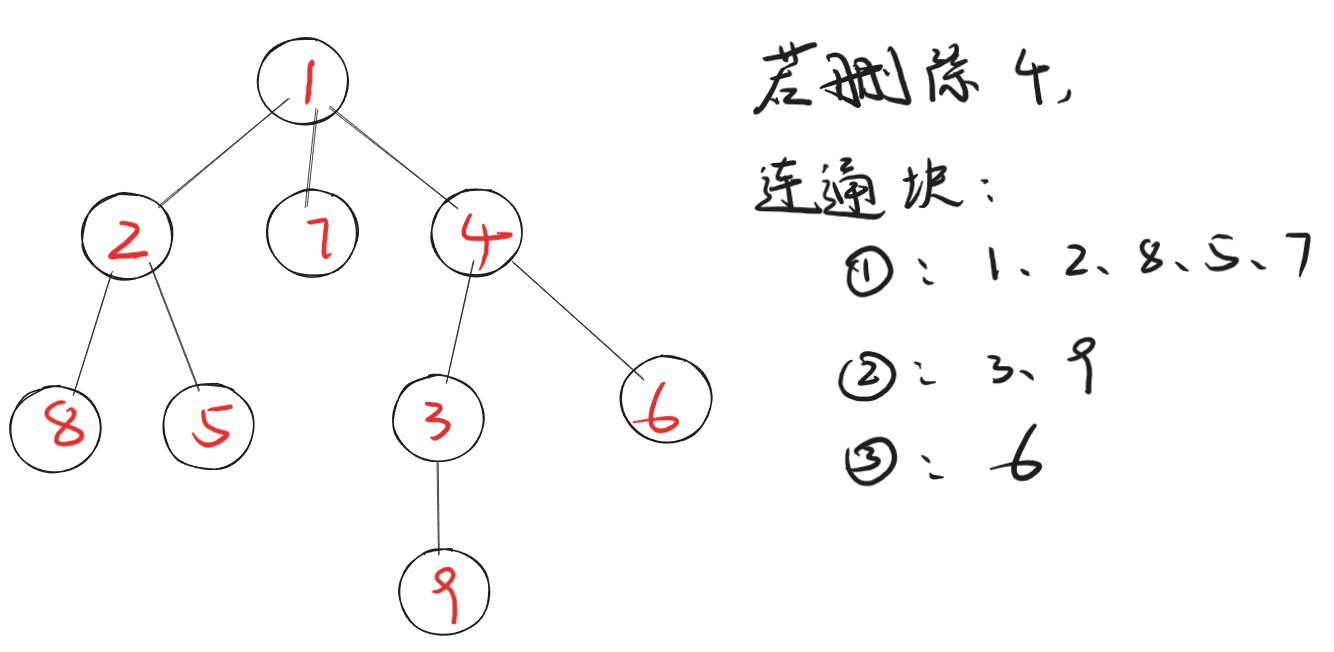
以节点 n-总结点数,这样我们就得知了所有连通块的数量,那么再对其求一个最小值即可。
示例代码
const int N = 1e5+5, M = N*2;
int n;
// h[i] 邻接表的表头节点,e[i]某个节点的信息,ne[i]节点i的
int h[N], e[M], ne[M], idx, ans=1e9;
bool st[N];
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs(int x) {
// x表示现在所在的节点
st[x] = 1; // 每个节点只走一次
int sum=1, res=0; // sum的作用是统计以x为根节点的树的总节点数
// res统计节点x的子树中,节点最多的点。
for (int i=h[x]; i!=-1; i=ne[i]) { // 遍历x这个节点的链表
int j = e[i]; // 访问当前节点
if (st[j]) continue; // 走过的就不走了
int num = dfs(j); // 搜索当前节点。
sum += num;
res = max(res, num);
}
res = max(res, n-sum); // 除了x的子树外,还有上面的其他节点
ans = min(res, ans);
return sum; // 返回最多的节点数
}
dfs(1);
BFS遍历
原理
如果理解了上面的DFS,那么广搜的原理其实也就基本一样,只是说在遍历的时候去搜索所有可以访问到的节点时,是通过循环去扫描邻接表,基本框架如下:
void bfs() {
q.push(首节点入队);
标记首节点已经访问;
while (q.size()) {
取出队首元素;
弹出队首元素;
for (int i=h[队首元素]; i!=-1; i=ne[i]) {
int j = e[i]; // 本次能访问到的元素
判断节点是否访问过,是则跳过;
否则节点入队,并标记已经访问过。
}
}
}
例题——图中点的层次
题目描述
给定一个
所有边的长度都是
请你求出
输入格式
第一行包含两个整数
接下来
输出格式
输出一个整数,表示
样例输入
4 5
1 2
2 3
3 4
1 3
1 4
样例输出
1
题目分析
无非就是BFS求最短路,只是遍历的方式略有改变,其余都是类似的,尝试自己写一下吧!
示例代码
核心代码(STL实现):
const int N = 1e5+5, M = N*2;
int h[N], e[M], ne[M], idx, n, m;
int st[N]; // 既可以标记是否访问,也可以记录最短距离
queue<int> q;
int bfs() {
memset(st, -1, sizeof st); // 初始都标记为-1,表示没访问过
q.push(1); // 首节点入队
st[1] = 0; // 记录步数,同时也可以标记是否访问过
while (q.size()) {
int now = q.front(); // 取出队首元素
q.pop(); // 队首元素出队
for (int i=h[now]; i!=-1; i=ne[i]) {
int j = e[i]; // ne[i]和h[i]中存的是下标,e[i]中是节点编号。
if (st[j] != -1) continue;
st[j] = st[now]+1;
q.push(j);
}
}
return st[n];
}
核心代码(数组模拟队列实现):
const int N = 1e5+5;
int h[N], e[N], ne[N], idx, n, m;
int q[N], st[N]; // st既可以标记是否访问,也可以记录最短距离
// q是队列
int bfs() {
memset(st, -1, sizeof st);
int hh=0, tt=-1;
q[++tt] = 1; // 首节点入队
st[1] = 0; // 记录步数,同时也可以标记是否访问过
while (hh <= tt) {
int now = q[hh++]; // 取出队首
for (int i=h[now]; i!=-1; i=ne[i]) {
int j = e[i]; // ne[i]和h[i]中存的是下标,e[i]中是节点编号。
if (st[j] != -1) continue;
st[j] = st[now]+1;
q[++tt] = j;
}
}
return st[n];
}
拓扑序列
拓扑序列是相对于有向图而言的,有向图的拓扑序列是其顶点的线性排序,使得对于每条有向边 (u, v),u 在序列中出现在 v 之前,下图展示了一个有向图的可能的拓扑序列:
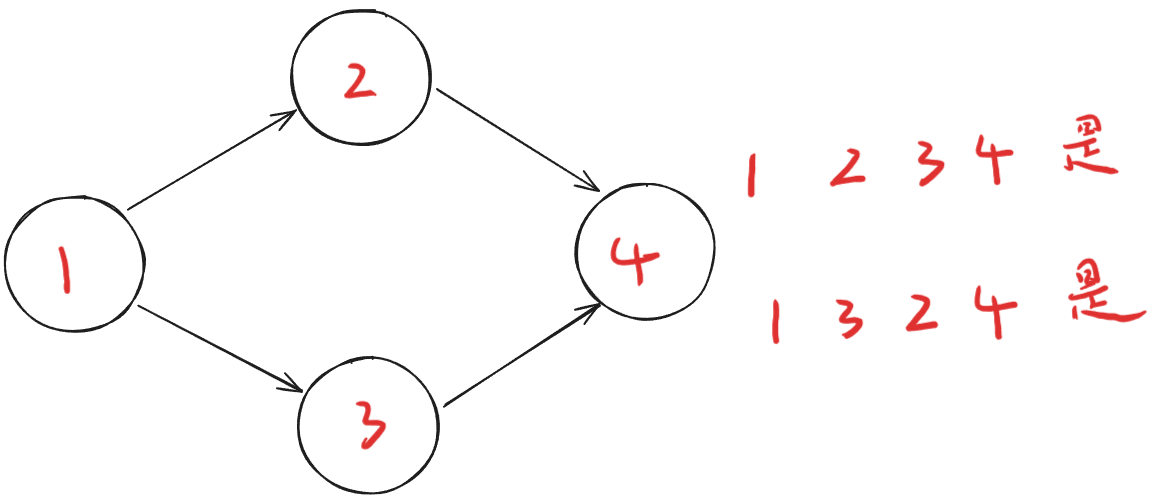
简单来说,拓扑序列需要满足几点:
- 每个顶点只出现一次。
- 对于图中的任何一条边,起点必须在终点之前。
所以拓扑序其实就是依次把入度为
来看一个例题:
例题——有向图的拓扑排序
题目描述
给定一个
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出
若一个由图中所有点构成的序列
输入格式
第一行包含两个整数
接下来
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出
样例输入
3 3
1 2
2 3
1 3
样例输出
1 2 3
题目分析
实现流程:
- 输入边时统计所有点的入度。
- 找到所有入度为
的点并入队。 - 依次出队,并在出队时搜索该节点连接的所有点,依次让这些点的入度减一。
- 如果某个点的入度减为
了,也入队。 - 最后检测是否所有的点都入队出队了。
示例代码
核心代码(STL实现):
const int N = 1e5+5;
int h[N], e[N], ne[N], idx, n, m;
int st[N]; // 统计节点i的入度
queue<int> q, res; // res是结果数组
bool topsort() {
for (int i=1; i<=n; i++) { // 入度为0的点入队
if (!st[i]) {
q.push(i);
res.push(i);
}
}
while (q.size()) {
int now = q.front();
q.pop();
for (int i=h[now]; i!=-1; i=ne[i]) {
int j = e[i];
st[j]--; // 删除这条边后,j节点的入度减1
if (st[j] == 0) { // 入度为0后则入队
q.push(j);
res.push(j);
}
}
}
return res.size() == n;
}
for (int i=1; i<=m; i++) {
cin >> a >> b;
add(a, b);
st[b]++; // 统计入度
}
if (topsort()) {
while (res.size()) { // 输出拓扑序列
cout << res.front() << " ";
res.pop();
}
}
else cout << -1;
核心代码(数组模拟队列实现):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int h[N], e[N], ne[N], idx, n, m;
int q[N], st[N]; // q是队列,st存储入度
bool topsort() {
int hh=0, tt=-1;
for (int i=1; i<=n; i++) {
if (!st[i])
q[++tt] = i;
}
while (hh <= tt) {
int t = q[hh++]; // 取出队首元素并出队。
for (int i =h[t]; i!=-1; i=ne[i]) {
int j = e[i];
st[j]--;
if (st[j] == 0) q[++tt] = j; // 入度为0则入队
}
}
return tt == n-1; // 如果为 n-1,说明所有节点都入队了。
}
if (topsort()) { // 数字其实全部都存在了 q 数组中。
for (int i=0; i<=n-1; i++) cout << q[i] << ' ';
}
else cout << -1;