广度优先搜索——BFS

基本概念

广度优先搜索(BFS)可以理解为“雨露均沾”，它就像雷达一样，一层一层的往外进行搜索，它会把当前层的所有节点搜索完后，再去搜索下一层的节点，下图展示了一个可能的广度优先搜索的顺序：

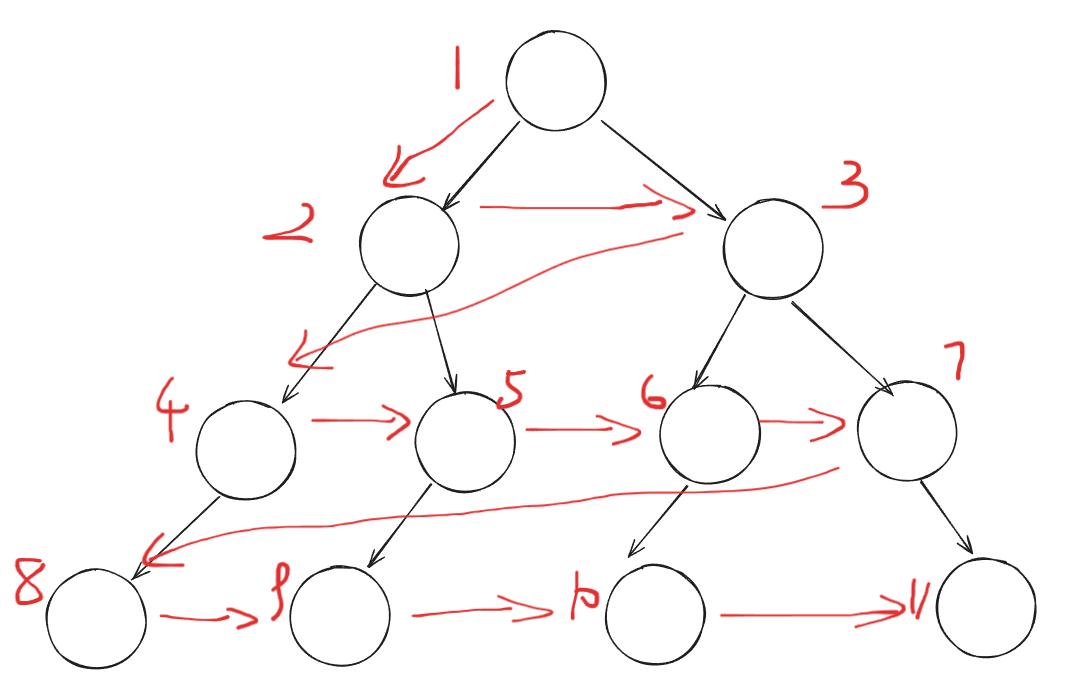
可以发现，在搜索的过程中是没有回溯的过程的，每个节点在用完之后就不会再出现了，也就是先来的节点就先出去了，这是什么的思想呢？没错，正是队列！

如何用队列的思想来具体描述上面的过程呢？如下所示：

节点1入队，此时队列为 [1]
节点1出队，并搜索节点1可以到达的所有节点，找到2和3
节点2和3入队，此时队列为 [2, 3]
节点2出队，并搜索节点2可以到达的所有节点，找到4和5
节点4和5入队，此时队列为 [3, 4, 5]
以此类推。。。

经典例题

例题——走迷宫

题目描述

给定一个 $n\times m$ 的二维整数数组，用来表示一个迷宫，数组中只包含 $0$ 或 $1$，其中 $0$ 表示可以走的路，$1$ 表示不可通过的墙壁。

最初，有一个人位于左上角 $(1,1)$ 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 $(n,m)$ 处，至少需要移动多少次。

数据保证 $(1,1)$ 处和 $(n,m)$ 处的数字为 $0$，且一定至少存在一条通路。

输入格式

第一行包含两个整数 $n$ 和 $m$。
接下来 $n$ 行，每行包含 $m$ 个整数（$0$ 或 $1$），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

样例输入

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

样例输出

8

题目分析

如果按照广搜的流程来搜索样例，那么流程如下，数字标号意为在第几层时搜索到这个节点。

代码流程：

初始节点入队;
while (队列不为空) {
	队首元素出队;
	查找所有队首元素可以访问到的节点, 依次入队;
	在查找过程中，可以顺便判断是否到达了终点，是则结束。
}

以上便是BFS代码的简单逻辑，而针对上面这个问题，我们还需要考虑几个点：

对于问题一，我们需要记住当前节点的 位置(几行几列)，以及 到达这个点走了几步。

对于问题二，因为该人只能往上下左右走，所以只需要依次访问当前格子的上下左右四个相邻格，判断能否走即可。

对于问题三，不建议访问，可以试想一下，如果第一步往下走，若可以访问之前的节点，那么第二步必然会有一个往上走的选项，那么搜索过程中就出现了大量多余的分支，降低了代码的效率。
所以，如果要避免这个问题，必然需要标记一下每个节点是否访问过。

对于问题四，如果当前访问的节点位置和终点位置一致，即到达了终点。

根据以上分析，你能尝试把代码写出来么？

示例代码

#include <bits/stdc++.h>
using namespace std;

struct P {
	int x, y, step;  // x,y表示行列，step表示步数 
};
queue<P> q;  // 用来实现广搜的队列 
int n, m;
int mp[105][105], vis[105][105];  // mp存储原始地图
// vis记录对应节点是否被访问过 
int d[5][2] = {{1,0}, {0,1}, {-1,0}, {0,-1}};
// 方向数组，用来控制上下左右移动。 

void bfs() {
	q.push(P{1, 1, 0});  // 初始节点入队
	vis[1][1] = 1;  // 标记为已访问
	while (!q.empty()) {
		P now = q.front();  // 获取队首元素
		q.pop();  // 队首元素出队
		if (now.x==n and now.y==m) {  // 到达终点 
			cout << now.step << '\n';
			return ;
		} 
		for (int i=0; i<4; i++) {
			int nx = now.x+d[i][0], ny = now.y+d[i][1];  // 计算相邻节点的位置
			if (nx<1 or nx>n or ny<1 or ny>m) continue;  // 越界了不处理 
			if (mp[nx][ny] or vis[nx][ny]) continue;  // 不能走不处理
			q.push(P{nx, ny, now.step+1});  // 节点入队 
			vis[nx][ny] = 1;  // 标记为已访问 
		}
	} 
} 

int main() {
	cin >> n >> m;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
			cin >> mp[i][j];
	bfs();
	return 0;
}

上述代码的时间复杂度为 $O(n\times m)$ ，因为每个点都只会搜索一次，而每个点会产生 $4$ 个子状态。

例题——八数码

题目描述

在一个 $3\times 3$ 的网格中，$1\sim 8$ 这 $8$ 个数字和一个 x 恰好不重不漏地分布在这 $3\times 3$ 的网格中。

例如：

1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 $3\times 3$ 的初始网格描绘出来。

例如，如果初始网格如下所示：

1 2 3 
x 4 6 
7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 $-1$。

样例输入

2 3 4 1 5 x 7 6 8

样例输出

19

题目分析

因为是只有 x 可以移动，所以可以把 x 的一次交换看作是一次移动，目标是从初始的状态移动到 12345678x 这个状态，问最少交换多少次，实际就是一个求最短路径的问题，只是移动的方式看起来不太一样，如下图所示。

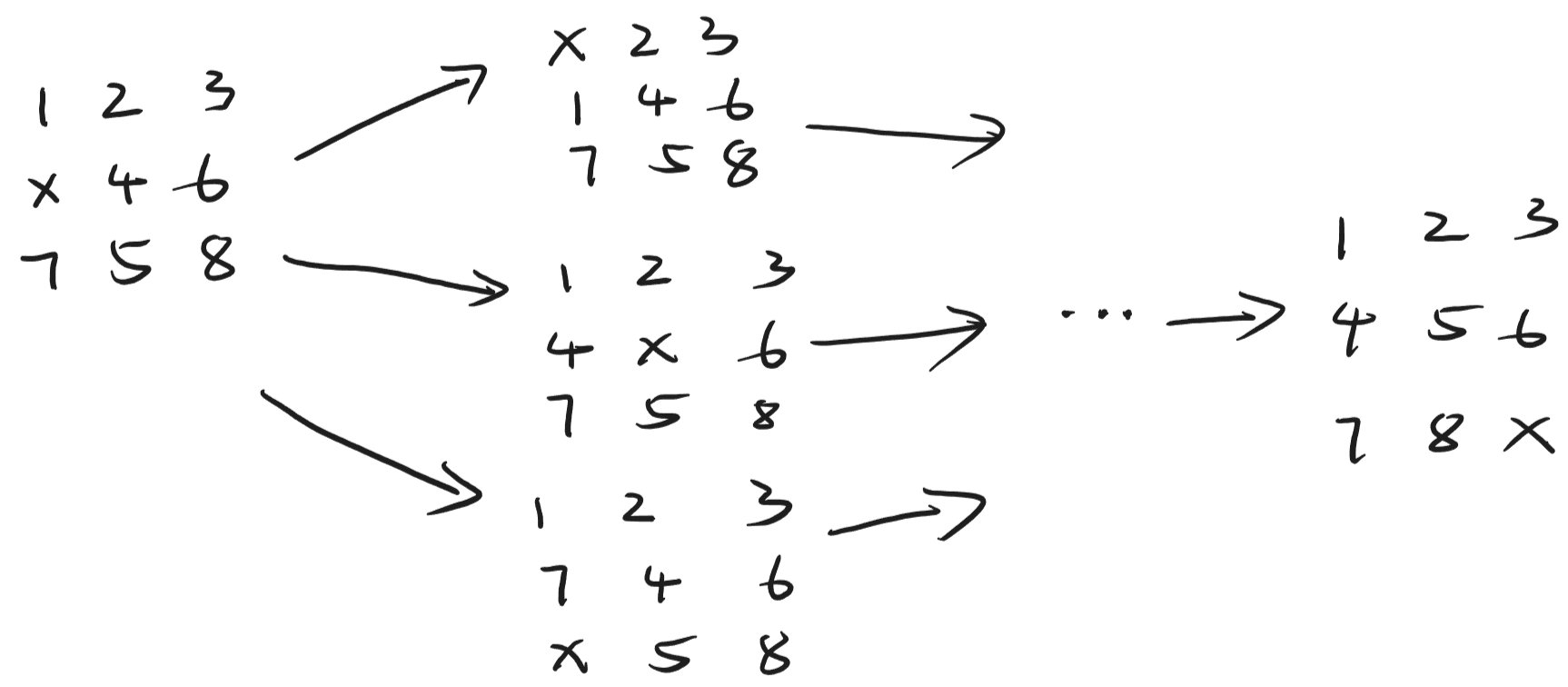
那么要思考的问题其实也很类似：

其一，肯定要记录 当前的棋盘状态、x 的位置、走的步数，关键在于状态如何存储？用二维数组来存当然可以，只是处理起来也稍显麻烦，因为固定是九个字符，所以直接用一个字符串存也是可以的。

其二，无非还是依次尝试把 x 和上下左右四个位置的字符进行交换，注意一下边界问题就好。

其三，肯定是不能访问的，但如何标记这个状态是否出现过呢？可以使用 map 或者 unordered_map 来建立字符串与数字的映射关系，让 map[s] 表示字符串 s 是否出现过，这也是为什么存储的时候要用字符串，也是方便后续使用 map 来标记。

其四，判断当前字符串和结果字符串 12345678x 是否相等即可。

根据以上分析，你能尝试把代码写出来么？

示例代码

#include <bits/stdc++.h>
using namespace std;
struct P {
	string s;  // 当前状态 
	int idx, st;  // idx是x当前的位置，st当前步数 
};
string res="12345678x";
queue<P> q;  // 用于广搜的队列
unordered_map<string, int> mp;  // 用于标记字符串是否出现过
int d[5][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};  // 上下左右

void bfs(string x) {
	q.push(P{x, x.find('x'), 0});
	mp[x] = 1;  // 标记已经走过
	while (q.size()) {
		P now = q.front();
		q.pop();
		if (now.s == res) {  // 判断是否到达终点
			cout << now.st;
			return ;
		}
		for (int i=0; i<4; i++) {
			// 将下标转换为行列形式，这样才好判断边界问题。
			int nx = now.idx/3+d[i][0], ny = now.idx%3+d[i][1], nidx;
			nidx = nx*3 + ny;  // 算出实际的下标
			if (nx<0 or nx>2 or ny<0 or ny>2) continue; 
			string ns = now.s;
			swap(ns[now.idx], ns[nidx]);  // 交换字符
			if (mp[ns]) continue;  // 判断这次的状态是否出现过
			q.push(P{ns, nidx, now.st+1});
			mp[ns] = 1;
		}
	} 
	cout << "-1";
}

int main() {
	char c;
	string x;
	for (int i=1; i<=9; i++) {
		cin >> c;
		x += c;
	}
	bfs(x);
	return 0;
}

总结

BFS实际就像地毯式搜索，一层一层地往外尝试所有可能的路线，这种搜索方式的流程实际就是 先进先出，所以一般BFS都使用队列来存储要搜索的节点；也正是因为这样的搜索方式，BFS在搜索最优解的问题上表现很优秀，例如最短路径、最少操作次数等等。
在使用BFS解决问题时，重点想清楚每个节点的状态应该如何表示，如何搜索到所有可能的新节点并入队，相信把这些设计清楚后，你会非常得心应手。