堆

基本概念

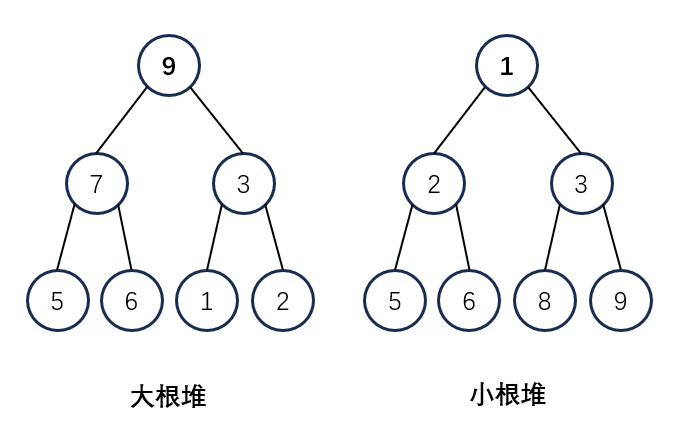
堆（Heap）是一种特殊的完全二叉树。当需要对一个动态变化的对象集合进行快速查找最大值或最小值时，使用堆。

性质：除叶子节点外每个节点的值都小于等于（或大于等于）其孩子节点的值。

Pasted image 20240326134140.png

堆数据结构的几个操作：

插入 insert()：将新元素插入堆中，并保持堆性质不变
查找堆顶元素 top()：返回堆顶元素
移除堆顶元素 pop()：删除堆顶元素
删除元素 remove()：删除堆中任意一个元素

STL堆（优先队列）

导入头文件和定义：

#include<queue>  // 也可以直接使用万能头
priority_queue <int> q;  // 默认是大根堆
priority_queue < int, vector<int>, greater<int> > p;  // 小根堆

基本操作：

empty   判断priority_queue是否为空，是返回true，否则false
pop     移除最大元素
push    添加元素到优先队列
size    返回队列中元素个数
top     返回对优先队列顶部最大元素的引用

数组模拟堆（小根堆）

1.存储与建堆

（1）基本性质和数组存储方式
以上图小根堆为例， $h [] = {0, 1, 2, 3, 5, 6, 10, 12}$

根节点编号（下标）为 $1$
$i$ 节点的左子节点编号为 $2 * i$
$i$ 节点的右子节点编号为 $2 * i + 1$
$i$ 节点的父节点编号为 $i / 2$

（2）建堆 $O (n)$
给定一个乱序数组 $a$ ，如何建堆？对每个元素执行一次插入操作，总时间复杂度为 $n l o g (n)$ ，但有更好的方法。

$h$ 为一颗完全二叉树，但对于当前的 $a$ ， $h$ 不一定满足堆的性质，我们可以从 $n / 2$ 的节点开始，对每个节点进行下滤。为什么是 $n / 2$ ，因为大于 $n / 2$ 的节点一定是叶子节点，叶子节点不存在下滤问题，它已经没有子节点了。

for (int i = n/2; i > 0; i--) down(i);

2.上滤up()和下滤 down()

上滤和下滤就是将某个节点向上或向下调整到合适的位置，使得整个堆满足其性质。由于堆是一颗完全二叉树，这两个操作的时间复杂度都是 O(logn)

void down(int u) {  // idx为当前数组用到的位置，也就是堆尾元素下标
	int t = u;
	if (2*u <= idx && h[2*u] < h[t]) t = 2*u;
	if (2*u <= idx && h[2*u+1] < h[t]) t = 2*u+1;
	if (t != u) {
		swap(h[t], h[u]);
		down(t);
	}
}

void up(int u) {
	if (u > 1 && h[u] < h[u/2]) {
		swap(h[u], h[u/2]);
		up(u/2);
	}        
}

3.基本操作

插入一个数 h[++idx] = x; up(idx);
求对象集合中的最小值 h[1];
删除最小值 h[1] = h[idx]; idx--; down(1);
删除任意一个元素 h[k] = h[idx]; idx--; up(k); down(k);
修改任意一个元素 h[k] = x; up(k); down(k);

例题：堆排序

题目描述

输入一个长度为 $n$ 的整数数列，从小到大输出前 $m$ 小的数。

输入格式

第一行包含整数 $n$ 和 $m$ 。
第二行包含 $n$ 个整数 $a_{i}$ ，表示整数数列。

数据范围： $1 \leq m \leq n \leq 10^{5}, 1 \leq a_{i} \leq 10^{9}$

输出格式

共一行，包含 $m$ 个整数，表示整数数列中前 $m$ 小的数。

输入样例

5 3
4 5 1 3 2

输出样例

1 2 3

题目分析

模板题

示例代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], cnt;

void down(int u) {
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        swap(h[u], h[t]);
        down(t);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;
    for (int i = n / 2; i; i -- ) down(i);
    while (m -- ) {
        printf("%d ", h[1]);
        h[1] = h[cnt -- ];
        down(1);
    }
    return 0;
}

例题：模拟堆

题目描述

维护一个集合，初始时集合为空，支持如下几种操作：

I x，插入一个数 x；
PM，输出当前集合中的最小值；
DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
D k，删除第 k 个插入的数；
C k x，修改第 k 个插入的数，将其变为 x；

现在要进行 $N$ 次操作，对于所有第 $2$ 个操作，输出当前集合的最小值。

输入格式

第一行包含整数 $N$ 。

接下来 $N$ 行，每行包含一个操作指令，操作指令为 I x，PM，DM，D k 或 C k x 中的一种。

数据范围： $1 \leq N \leq 10^{5}, - 10^{9} \leq x \leq 10^{9}$ ，数据保证合法。

输出格式

对于每个输出指令 PM，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

输入样例

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例

-10
6

题目分析

模板题进阶。

几个重点：

idx

就数组模拟堆来说，知道数组的下标就知道节点在堆中的位置，所以核心就在于即使有 down 和 up 操作也能维护堆数组的下标 k 和节点 idx 的映射关系。

$p h$ 数组表示 $p h [i d x] = k$ ，从节点映射到下标，节点值为 $h [p h [i d x]]$ ，左儿子 $h [p h [i d x] * 2]$ ，右儿子 $h [p h [i d x] * 2 + 1]$

hp数组和ph数组

$p h$ 数组主要用于帮助从 $i d x$ 映射到下标 $k$ ， $h p$ 数组是存的 $k$ 到 $i d x$ 的映射。

示例代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 100010;

int h[N], ph[N], hp[N], cnt;

void heap_swap(int a, int b) {
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u) { // 下滤
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u) {  // 上滤
    while (u / 2 && h[u] < h[u / 2]) {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main() {
    int n, m = 0;
    scanf("%d", &n);
    while (n -- ) {
        string op;
        int k, x;
        cin >> op;
        if (op == "I") {
            scanf("%d", &x);
            cnt ++ ;
            m ++ ;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        else if (op == "PM") printf("%d\n", h[1]);
        else if (op == "DM") {
            heap_swap(1, cnt);
            cnt -- ;
            down(1);
        }
        else if (op == "D") {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, cnt);
            cnt -- ;
            up(k);
            down(k);
        }
        else {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }
    return 0;
}