链表

基本概念

链表（Linked List）是一种常见的线性数据结构，它由一系列节点组成，每个节点包含数据域和指针域。每个节点的指针指向下一个节点，形成了节点之间的链接。

链表可以分为多种类型，包括单向链表、双向链表和循环链表等。其中：

单向链表：每个节点只包含一个指针，指向下一个节点。
双向链表：每个节点包含两个指针，分别指向前一个节点和后一个节点。
循环链表：链表中最后一个节点的指针指向链表的头节点，形成一个环形结构。

链表相比于数组具有动态的内存分配和插入删除操作的优势，但在访问元素时效率较低，因为需要从头节点开始逐个遍历。链表通常用于需要频繁的插入删除操作或者不需要随机访问的场景。

链表的基本操作包括：

在链表头部插入节点（头插法）。
在链表尾部插入节点（尾插法）。
在指定位置插入节点。
删除指定位置的节点。
获取链表长度。
遍历链表并访问节点数据。

链表在计算机科学中有着广泛的应用，例如作为其他数据结构的基础，如栈、队列、图等，后面我们学习图算法时，就是用邻接表来存储图数据。

单链表——数组模拟

例题：单链表

题目描述

实现一个单链表，链表初始为空，支持三种操作：

1.向链表头插入一个数；
2.删除第 k 个插入的数后面的数；
3.在第 k 个插入的数后插入一个数。

现在要对该链表进行 $M$ 次操作，进行完所有操作后，从头到尾输出整个链表。

注意：题目中第 $k$ 个插入的数并不是指当前链表的第 $k$ 个数。例如操作过程中一共插入了 $n$ 个数，则按照插入的时间顺序，这 $n$ 个数依次为：第 $1$ 个插入的数，第 $2$ 个插入的数，... ，第 $n$ 个插入的数。

输入格式

第一行包含整数 $M$ ，表示操作次数。

接下来 $M$ 行，每行包含一个操作命令，操作命令可能为以下几种：

1.H x，表示向链表头插入一个数 x。
2.D k，表示删除第 k个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
3.I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。

数据范围： $1 \leq M \leq 100000$ ，所有操作保证合法。

输出格式

共一行，将整个链表从头到尾输出。

输入样例

输出样例

6 4 6 5

题目分析

链表由多个节点构成，单链表的每个节点需要存储两项信息：数据值和下一个节点的位置。

我们用两个数组分别来存储值和指针：

e[] 存储当前节点的值。

ne[] 存储下一个节点的地址（下标）。

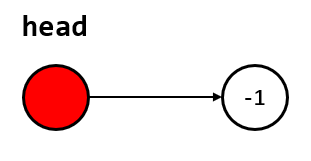
ne[] 和 e[] 通过下标来关联，我们一般在初始化的时候会创建一个 idx 指针变量，并初始化为 1，同时借助 head 变量表示头节点，而尾节点一般用 -1 表示。

（1）初始化一个单链表

Pasted image 20240403193312.png

const int N = 1e5+10;
int e[N], ne[N], idx, head;

// 初始化, 从下标1开始用，idx为几就表示使用到当前第几个点
void init() {
    head = -1;
    idx = 1;
}

（2）在头节点后面插入一个新节点

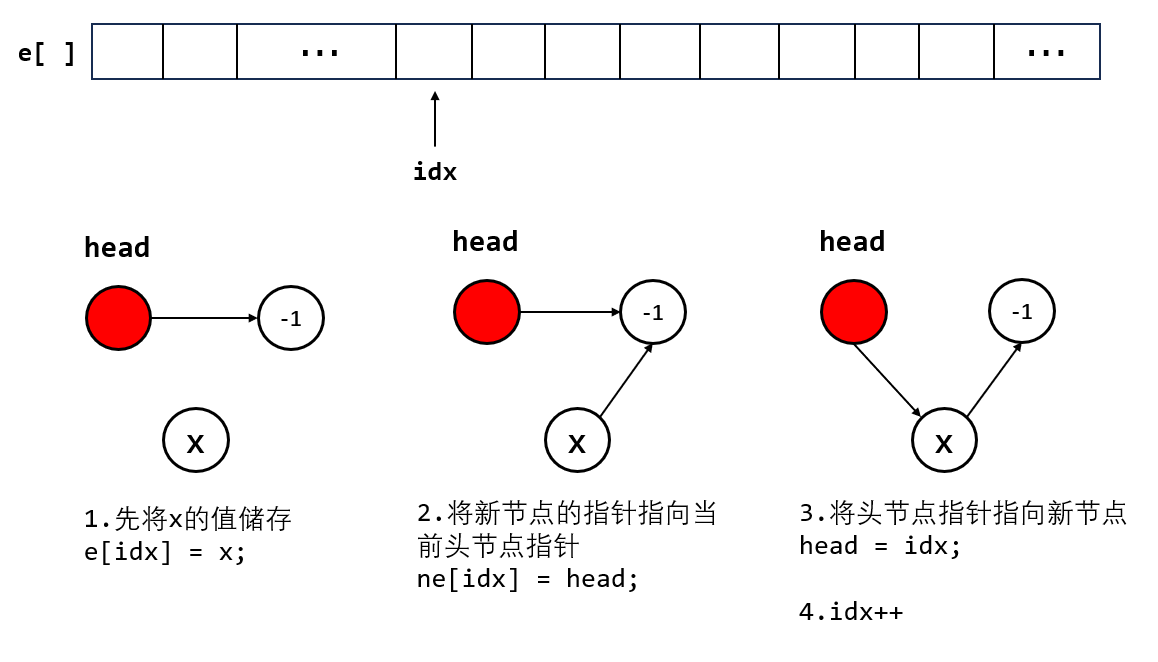
Pasted image 20240403200045.png

// 插入到头节点后面
void add_to_head(int x) {
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx ++;
}

（3）在第k个点后面插入一个新节点

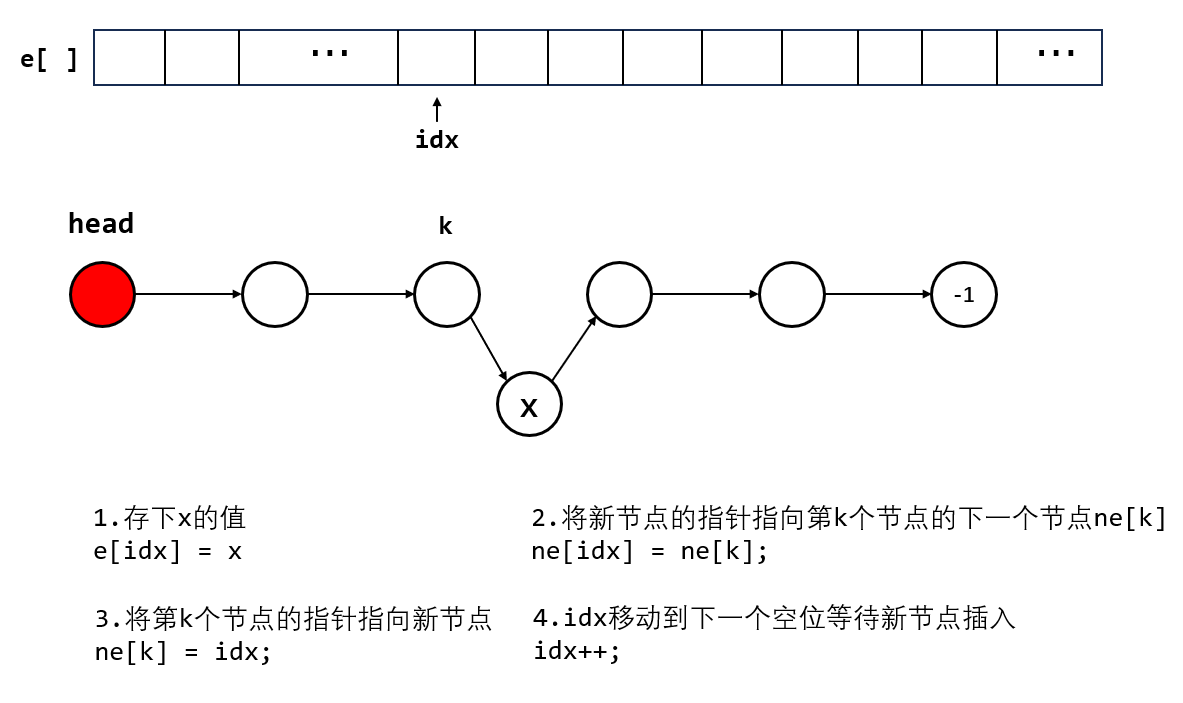
Pasted image 20240403200709.png

// 在第k个点后插入一个点x
void add_to_k(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx ++;
}

（4）删除第k个插入的点后面的点

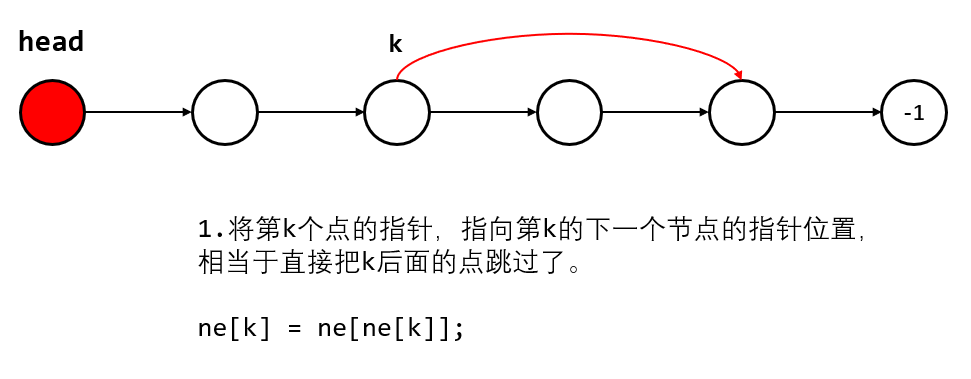
Pasted image 20240403201054.png

// 删除第k个插入的点后面的点
void remove(int k) {
    if (k == 0) head = ne[head]; // 0表示删除头节点
    ne[k] = ne[ne[k]];
}

示例代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+10;
int e[N], ne[N], idx, head;

// 初始化, 从下标1开始用，idx为几就表示使用到当前第几个点
void init() {
    head = -1;
    idx = 1;
}
// 删除第k个插入的点后面的点
void remove(int k) {
    if (k == 0) head = ne[head]; // 0表示删除头节点
    ne[k] = ne[ne[k]];
}
// 在第k个点后插入一个点x
void add_to_k(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx ++;
}
// 插入到头节点后面
void add_to_head(int x) {
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx ++;
}

int main() {
    init();
    int m, k, x;
    cin >> m;
    while (m -- ) {
        char op;
        cin >> op;
        if (op == 'H') {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'I') {
            cin >> k >> x;
            add_to_k(k, x);
        }
        else {
            cin >> k;
            remove(k);
        }
    }
    for (int i = head; i != -1; i = ne[i]) cout << e[i] << " ";
    
    return 0;
}

双链表——数组模拟

例题：双链表

题目描述

实现一个双链表，双链表初始为空，支持 $5$ 种操作：

1.在最左侧插入一个数；
2.在最右侧插入一个数；
3.将第 k 个插入的数删除；
4.在第 k 个插入的数左侧插入一个数；
5.在第 k 个插入的数右侧插入一个数

现在要对该链表进行 $M$ 次操作，进行完所有操作后，从左到右输出整个链表。

输入格式

第一行包含整数 $M$ ，表示操作次数。

接下来 $M$ 行，每行包含一个操作命令，操作命令可能为以下几种：

1.L x，表示在链表的最左端插入数 x。
2.R x，表示在链表的最右端插入数 x。
3.D k，表示将第 k 个插入的数删除。
4.IL k x，表示在第 k 个插入的数左侧插入一个数。
5.IR k x，表示在第 k 个插入的数右侧插入一个数。

数据范围： $1 \leq M \leq 100000$ ，所有操作保证合法。

输出格式

共一行，将整个链表从左到右输出。

输入样例

10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2

输出样例

8 7 7 3 2 9

题目分析

链表由多个节点构成，双链表的每个节点需要存储三项信息：数据值、前一个节点的位置、下一个节点的位置。

我们用三个数组分别来存储值和 左指针、右指针：

e[] 存储当前节点的值

l[] 存储前一个节点的地址（下标）

r[] 存储后一个节点的地址（下标）

e[]、l[]、r[]通过下标来关联，我们一般在初始化的时候会创建一个 idx 指针变量，并初始化为 1，同时借助 head 和 tail 变量来表示双链表的头节点与尾节点。

（1）初始化双链表

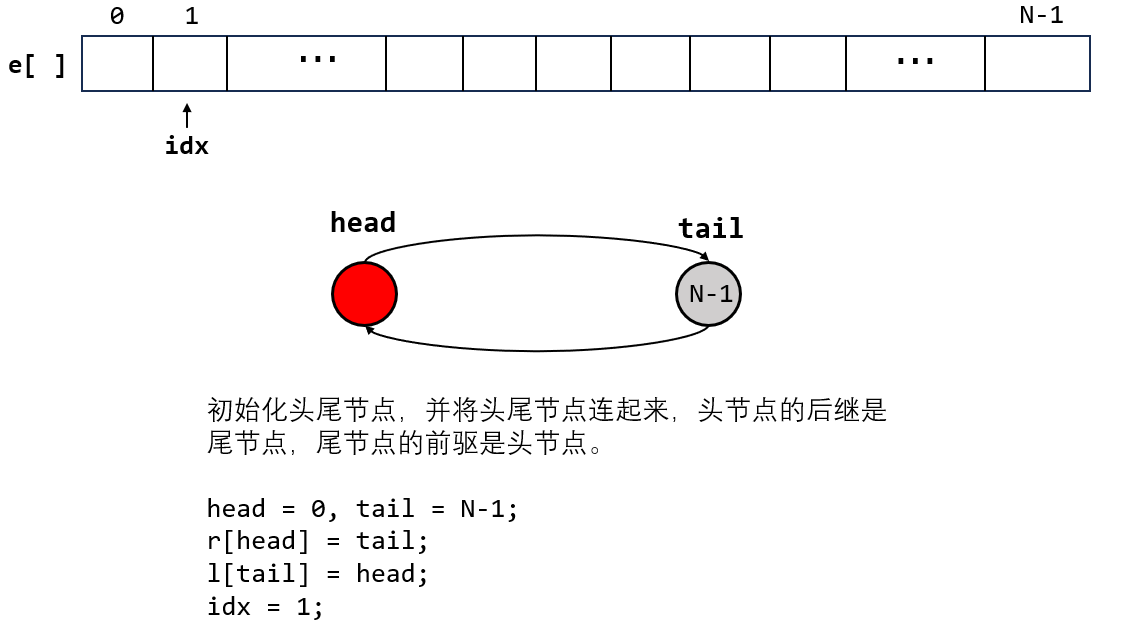
Pasted image 20240403202514.png

（2）在第 k 个点的后面插入一个值为 x 的新节点

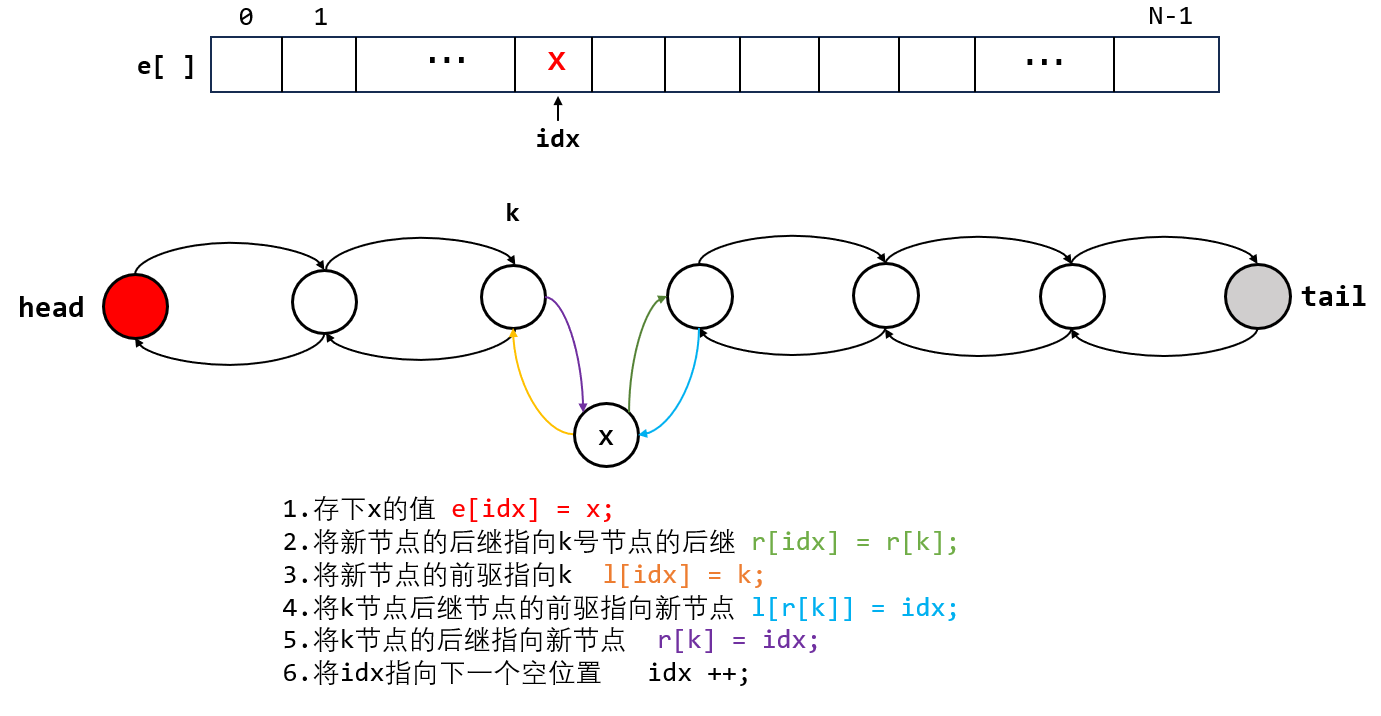
Pasted image 20240403204314.png

若想要在第 k 个点的前一个点插入呢？只需要通过 k 访问到 l[k] 再进行同样的操作即可。

（3）将第k个点删除

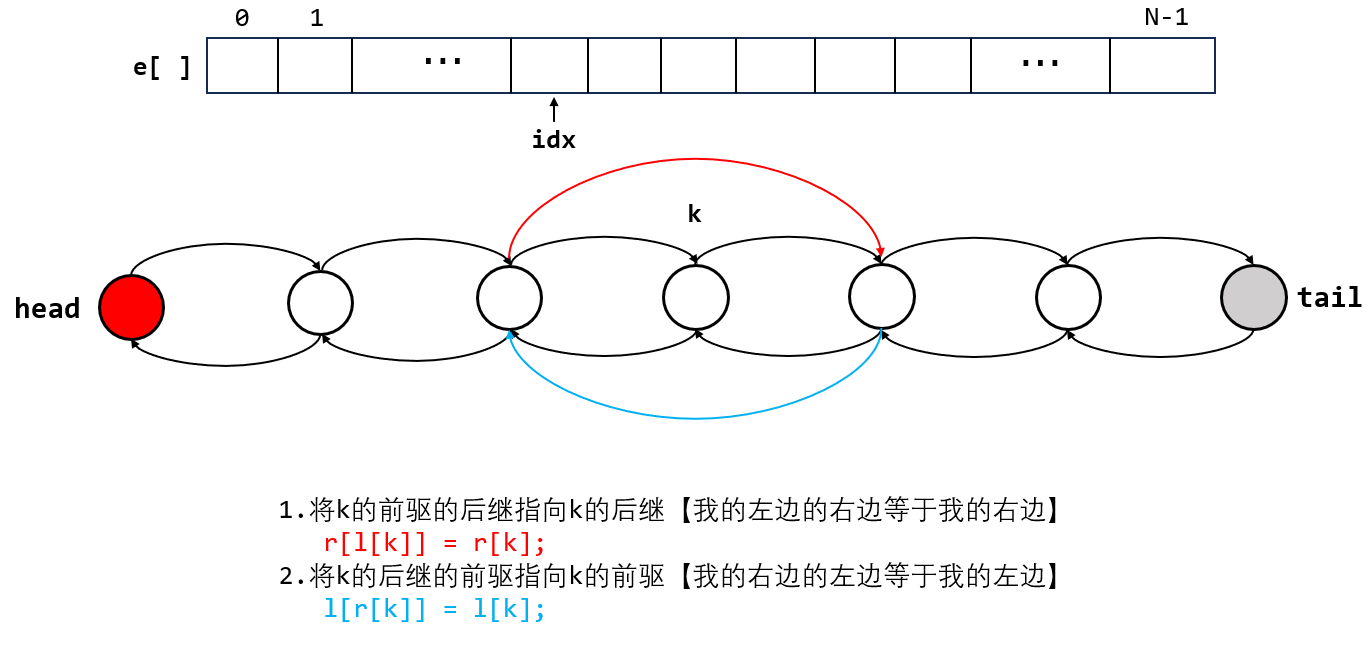
Pasted image 20240403204825.png

示例代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5+10;
int l[N],r[N],e[N],idx,head,tail; // 当前点的左地址，右地址，值，地址

void init() {
    head = 0, tail = N-1;
    r[head] = tail;
    l[tail] = head;
    idx = 1; 
}

// 在第k个点的右边插入一个点x，第k个点的地址就是k。
void add(int k, int x) {
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx;
    idx ++;
}
// 删除第k个点
void remove(int k) {
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

int main() {
    init();
    int m, k, x;
    cin >> m;
    while (m -- ) {
        string op;
        cin >> op;
        if (op == "L") {
            cin >> x;
            add(head, x);
        }
        else if (op == "R") {
            cin >> x;
            add(l[tail], x);
        }
        else if (op == "IL") {
            cin >> k >> x;
            add(l[k], x);
        }
        else if (op == "IR") {
            cin >> k >> x;
            add(k, x);
        }
        else {
            cin >> k;
            remove(k);
        }
    }
    
    for (int i = r[head]; i != tail; i = r[i]) cout << e[i] << " ";
    
    return 0;
}