栈与队列

栈

基本概念

栈（Stack）是一种基于 后进先出(LIFO) 原则的数据结构，它是一种线性表。栈具有两个主要操作：压入 (Push) 和弹出 (Pop)。

压入操作在栈顶插入新元素，而弹出操作则将栈顶元素移除。栈常用于需要临时存储和后进先出访问数据的场景，如函数调用、表达式求值、括号匹配等。

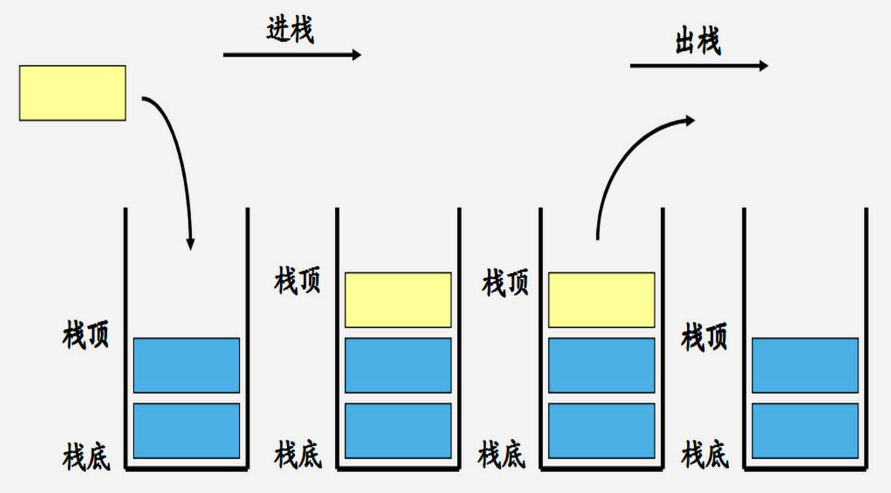
数组模拟栈

下面演示了用数组来模拟栈的各种常规操作，数组模拟的栈相较STL来说，速度更快，且支持一些 “非常规” 的操作，在进行 debug 或者某些特殊操作时往往有奇效。

const int N = 1e5 + 10; // 栈空间大小
// tt为栈顶指针，初始为0，表示栈空
stk[N], tt; 
// 入栈
stk[++tt] = x;
// 出栈
tt --;
// 返回栈顶元素
cout << stk[tt];
// 判断栈是否为空
if (tt == 0) ...
// 当前栈内元素个数
cout << tt;

STL stack

C++ 的 STL 中也提供了栈，同样具备了各种栈的常规操作，使用起来不容易错。

#include<stack>
stack<int> stk;  // 创建int类型栈，名字为stk
stk.push(x)      // 把x压栈
stk.pop()        // 弹出栈顶元素
stk.top()        // 查看栈顶元素
stk.size()       // 返回栈内元素个数
stk.empty()      // 返回栈是否为空

两种实现方法都需要掌握，平时练习时尽量多用数组模拟实现。

例题：模拟栈

题目描述

实现一个栈，栈初始为空，支持四种操作：

push x – 向栈顶插入一个数 x；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。

现在要对栈进行 $M$ 个操作，其中的每个操作 $3$ 和操作 $4$ 都要输出相应的结果。

输入格式

第一行包含整数 $M$ ，表示操作次数。

接下来 $M$ 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

数据范围： $1 \leq M \leq 100000$ ， $1 \leq x \leq 10^{9}$

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

输入样例

10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty

输出样例

5
5
YES
4
NO

题目分析

模板题，使用数组模拟实现栈的功能即可。

示例代码

#include <iostream>
using namespace std;
const int N = 1e5 + 10;

int m;
int stk[N], tt;

int main() {
    cin >> m;
    while (m -- ) {
        string op;
        int x;
        cin >> op;
        if (op == "push") {
            cin >> x;
            stk[ ++ tt] = x;
        }
        else if (op == "pop") tt-- ;
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }
    return 0;
}

表达式计算前置知识

前缀、中缀、后缀表达式

前缀、中缀和后缀表达式是数学和计算机科学中常见的表示数学表达式的方式。它们分别描述了操作符和操作数在表达式中的排列方式。

中缀表达式：中缀表达式是我们最常见的数学表达式形式，操作符位于操作数的中间。例如：(3 + 4) * 5。中缀表达式通常需要使用括号来明确操作符的优先级。
前缀表达式（也称为波兰前缀表达式）：在前缀表达式中，操作符位于其操作数之前。例如：* + 3 4 5。前缀表达式不需要括号来确定运算顺序，因为操作符在前，所以很清晰地知道每个操作符操作的对象是哪些。
后缀表达式（也称为逆波兰表达式）：在后缀表达式中，操作符位于其操作数之后。例如：3 4 + 5 *。后缀表达式同样不需要括号来确定运算顺序。

中缀表达式：(A + B) * C - D

对应的前缀表达式：- * + A B C D

对应的后缀表达式：A B + C * D -

中缀表达式需要括号来表示运算优先级，而前缀和后缀表达式通过操作符的位置来表示运算的顺序，因此它们在计算机科学中更容易处理。一种比较容易的中缀转前后缀的方法是：

补全所有中缀表达式的括号，(((A + B) * C) - D)
将括号里面的运算符提到属于自己的括号外，前缀就移到对应括号的前面，后缀就移到后面。

拓展

中缀转后缀通用规则

会有一个符号栈用来存储运算符。

从左至右扫描中缀表达式的每个字符。

如果遇到数字，则直接将其加入后缀表达式(输出)。
如果遇到运算符，则比较它和符号栈的栈顶运算符的优先级。
如果栈为空，或者当前运算符优先级大于栈顶运算符，或者栈顶是左括号则将其直接入栈。
如果运算符优先级小于或等于栈顶运算符，则弹出栈顶运算符，并将其加入后缀表达式，然后重新执行步骤二。
如果遇到左括号，直接入栈
如果遇到右括号，则不断弹出栈顶运算符，并且加入后缀表达式，直到遇到左括号，然后把左括号丢弃。
扫描完成后，将栈中剩余的运算符依次弹出并加入后缀表达式。

中缀转前缀通用规则

会有一个符号栈用来存储运算符，结果栈存储转换的结果。

从右至左扫描中缀表达式的每个字符。

如果遇到数字，则直接将其加入结果栈。
如果遇到运算符，则比较它和符号栈的栈顶运算符的优先级。
如果栈为空，或者当前运算符优先级大于等于栈顶运算符，或者栈顶是右括号则将其直接入符号栈。
如果运算符优先级小于栈顶运算符，则弹出栈顶运算符，并将其加入结果栈，然后重新执行步骤二。
如果遇到右括号，直接入符号栈
如果遇到左括号，则不断弹出符号栈顶运算符，并且加入结果栈，直到遇到右括号，然后把右括号丢弃。
扫描完成后，将栈中剩余的运算符依次弹出并加入结果栈。
将结果栈栈顶依次弹出并输出，得到的式子就是前缀表达式。

挑战一下

转换一下这几个表达式吧：

2*(9+6/3-5)+4
4+3/2-5+(7+2*3)/4

除此之外，也可以利用表达式树来实现转换。

表达式树(语法树)

表达式树是一种树形数据结构。在表达式树中，每个节点都代表一个操作符或操作数，操作符位于内部节点，而操作数位于叶子节点。通过组合操作符和操作数，表达式树可以表示复杂的数学表达式。

语法树的构造步骤：

从当前的中缀表达式中选择最后执行的四则运算符，作为当前的根节点，若没有运算符，则将数字写在对应的节点处；
该运算符将中缀表达式分为左右两部分，即左右子树，然后对左右子树再分别重复步骤1。

以 (A + B) * C - D 为例，表达式树如下：

操作数均位于叶子节点，而操作符均为内部节点。遍历一颗表达式树有三种方式：前序遍历、中序遍历、后序遍历。

前序：根左右 ==> 对应前缀表达式

中序：左根右 ==> 对应中缀表达式

后序：左右根 ==> 对应后缀表达式

前中后缀表达式的计算方法

【计算前缀】
从后往前遍历表达式，遇到数字入栈，遇到运算符弹出栈顶两个元素进行运算，若为减法或除法运算，第一个弹出元素作为被减数或者被除数。再把运算结果重新压入栈。

【计算后缀】
从前往后遍历表达式，遇到数字入栈，遇到运算符弹出栈顶两个元素进行运算，若为减法或除法运算，第二个弹出元素作为被减数或者被除数。再把运算结果重新压入栈。

【计算中缀】
需要两个栈，一个数字栈，一个符号栈，具体操作方法我们通过后面的习题来学习。

例题：后缀表达式求值

题目描述

从键盘读入一个后缀表达式（字符串），只含有 $0 - 9$ 组成的运算数及加（+）、减（—）、乘（*）、除（/）四种运算符。每个运算数之间用一个空格隔开，不需要判断给你的表达式是否合法。以 @ 作为结束标志。

提示：输入字符串长度小于 $250$ ，参与运算的整数及结果之绝对值均在 $2^{64}$ 范围内，如有除法保证能整除。

输入格式

共一行，为给定表达式。表达式的长度不超过 $250$ 。

输出格式

共一行，为表达式的结果。

输入样例

16 9 4 3 +*-@

输出样例

-47

题目分析

后缀表达式的计算规则：从前往后遍历表达式：

遇到数字，数字入栈。
遇到运算符，弹出栈顶两个数字进行运算，若为减法或除法运算，第二个弹出元素作为被减数或者被除数。再把运算结果重新压入栈。

按照以上规则进行模拟即可。

示例代码

#include <bits/stdc++.h>  
using namespace std;  
const int N = 255;  
int st[N], hh, len;  
string s;  
  
void calc(char opt) {  
    // 从栈顶取出两个元素  
    int num2 = st[hh--];  
    int num1 = st[hh--];  
    int x = 0;  
    if (opt == '+') x = num1 + num2;  
    else if (opt == '-') x = num1 - num2;  
    else if (opt == '*') x = num1 * num2;  
    else x = num1 / num2;  
    st[++hh] = x;  
}  
  
int main() {    
    getline(cin, s);  
    len = s.size();  
    // len-1是不去管 @  
    for (int i = 0; i < len - 1; i++) {  
        if (isdigit(s[i])) {  
            int num = 0;  
            while (isdigit(s[i])) {  
                num = num * 10 + s[i] - '0';  
                i++;  
            }  
            i--;  // 多加了一位，要去掉影响  
            st[++hh] = num;  // 数字入栈  
        } else if (s[i] != ' ') {  
            calc(s[i]);  
        }  
    }  
    cout << st[1];  
    return 0;  
}

例题：中缀表达式求值

题目描述

给定一个表达式，其中运算符仅包含 +,-,*,/（加减乘整除），可能包含括号，请你求出表达式的最终值。

注意：

数据保证给定的表达式合法。
题目保证符号 - 只作为减号出现，不会作为负号出现，例如，-1+2,(2+2)*(-(1+1)+2) 之类表达式均不会出现。
题目保证表达式中所有数字均为正整数。
题目保证表达式在中间计算过程以及结果中，均不超过 $2^{31} - 1$ 。
题目中的整除是指向 $0$ 取整，也就是说对于大于 $0$ 的结果向下取整，例如 $5 / 3 = 1$ ，对于小于 $0$ 的结果向上取整，例如 $5 / (1 - 4) = - 1$ 。

输入格式

共一行，为给定表达式。表达式的长度不超过 $10^{5}$ 。

输出格式

共一行，为表达式的结果。

输入样例

(2+2)*(1+1)

输出样例

题目分析

中缀表达式对应中序遍历，以样例为例，表达式树如下：

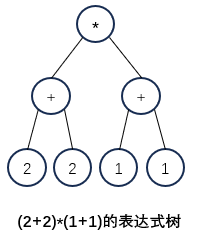
Pasted image 20240327153430.png

*,/ 的优先级大于 +,- 优先级；同优先级，从左往右算；括号优先级大于其他。

所有的数字都在叶子节点，运算符都是根节点，括号不作为节点，但需要作为运算符参与运算符优先级的比较。

中序遍历的计算过程，对任意一颗表达式树有：

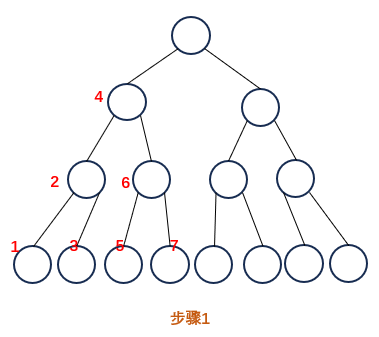
Pasted image 20240327155136.png

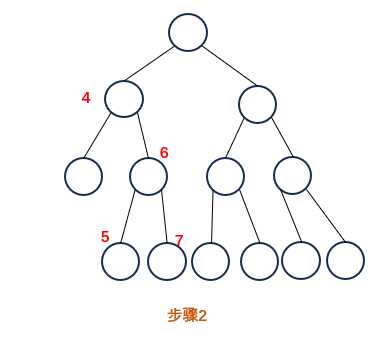
Pasted image 20240327155213.png

遍历完 1、2、3 号节点后，4号的左子树遍历完毕，计算出 4 的左子树结果，新节点作为 4 的左孩子

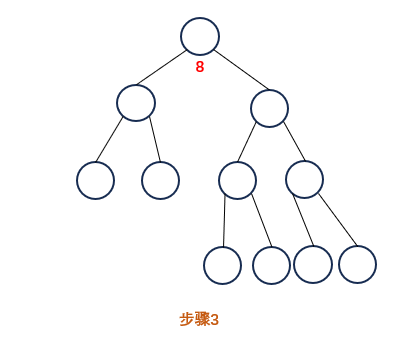
Pasted image 20240327155236.png

遍历完5 6 7号节点后，4的右子树遍历完毕，计算出4的右子树结果，新节点作为4的右孩子

Pasted image 20240327155300.png

新的左右孩子计算出结果，作为 8 的左子节点

Pasted image 20240327155328.png

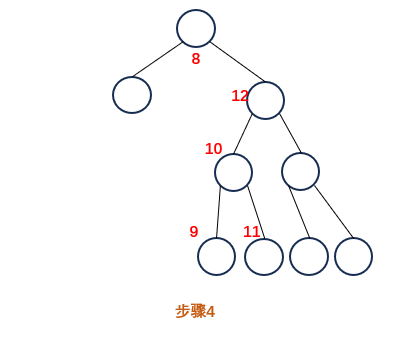
遍历完9 10 11号节点后，12的左子树遍历完毕，计算出 12 的左子树结果，新节点作为 12 的左孩子

Pasted image 20240327155359.png

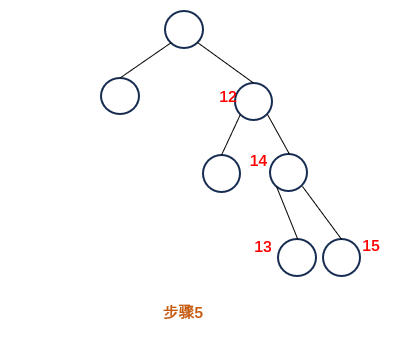
遍历完13 14 15号节点后，12的右子树遍历完毕，计算出12的右子树结果，新节点作为12的右孩子

Pasted image 20240327155421.png

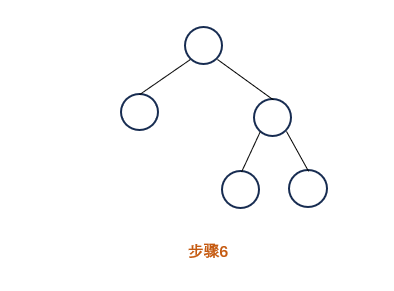
新的左右孩子计算出结果，作为 8 的右子节点

Pasted image 20240327155448.png

遍历 8 的左右子节点，得到最终结果

计算过程分析：
如何判断某棵子树是否被遍历完了？

中序遍历往上走时，子树遍历完，例如过程1中遍历4号节点时，1 2 3 的子树遍历完了。
中序遍历往下走时，子树未遍历完，例如过程2中遍历节点6时，相对4是往下走的，此时8的左子树未遍历完。

一个中缀表达式，转换成表达式树后，高优先级运算符一定是在低优先级运算符下面，所以我们可以通过运算符的优先级来判断是否在往上走，以此判断是否遍历完了某棵子树。

当前运算符的优先级 <= 上一运算符的优先级时，往上走
当前运算符的优先级 >= 上一运算符的优先级时，往下走

当往上走时，说明当前子树已经遍历完，需要计算子树的结果，并将此结果作为新节点代替原来的子树。

问题解法：

创建一个数字栈，用来存放运算数

创建一个符号栈，用来存放运算符

遍历表达式字符串，会遇到以下几种情况：

数字：压入数字栈，数字不会产生计算过程，所以只需提取数字，并压入数字栈
括号：
1. 遇到左括号，一定往下走，只需将左括号压入符号栈
2. 遇到右括号，说明会往上走，此时需要计算括号表示的子树结果，直到遇到左括号
普通二元运算符：
1. 往下走，将当前运算符压入符号栈
2. 往上走，计算上一运算符，直到栈为空或当前运算符优先级 > 上一运算符

示例代码

#include<iostream>
#include<stack>
#include<unordered_map>
using namespace std;

stack<int> num;
stack<char> op;

void eval() {
	int b = num.top(); num.pop();
	int a = num.top(); num.pop();
	char c = op.top(); op.pop();
	int x;
	if (c == '+') x = a + b;
	else if (c == '-') x = a - b;
	else if (c == '*') x = a * b;
	else x = a / b;
	num.push(x);
}

unordered_map<char, int> pr{{'+',1},{'-',1},{'*',2},{'/',2}};

int main() {
	string str;
	cin >> str;
	for (int i = 0; i < str.size(); i++) {
		auto c = str[i];
		if (isdigit(c)) {
			int x = 0, j = i;
			while (j < str.size() && isdigit(str[j]))
			{
				x = x * 10 + str[j] - '0';
				j++;
			}
			i = j - 1;
			num.push(x);
		}
		else if (c == '(') op.push(c);
		else if (c == ')') {
			while (op.top() != '(') eval();
			op.pop();
		}
		else {
			while (op.size() && op.top() != '(' && pr[c] <= pr[op.top()])
				eval();
			op.push(c);
		}
	}
	while (op.size()) eval();
	cout << num.top();
	return 0;
}

队列

基本概念

队列（Queue）是一种常见的数据结构，它遵循 先进先出（FIFO）的原则。队列有两个主要的操作：

入队（Enqueue）：向队尾插入新元素。
出队（Dequeue）：从队头移除元素。

除了这两个基本操作外，队列通常还包括以下操作：

队列判空（IsEmpty）：检查队列是否为空。
队列长度（Size）：获取队列中元素的个数。
获取队头元素（Front）：获取队头元素的值，但不移除它。

队列常用于模拟排队、任务调度等场景。在后续算法学习中，BFS广度优先搜索也要借助队列来实现。

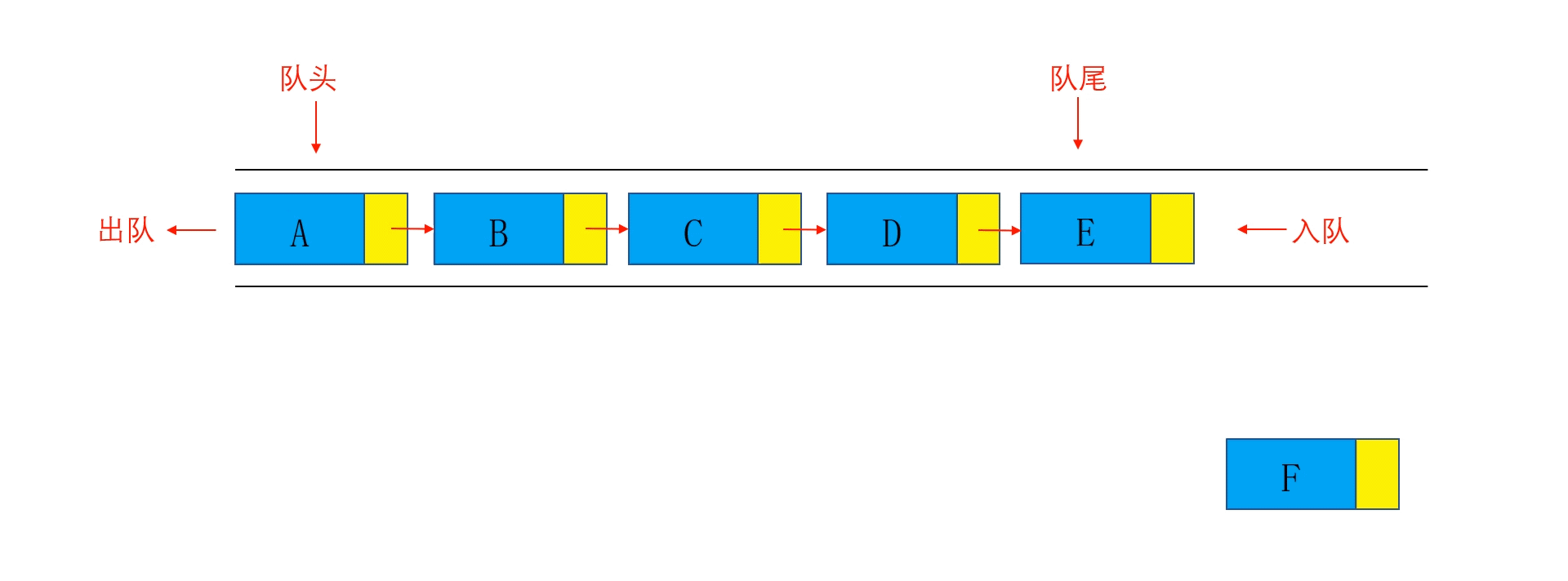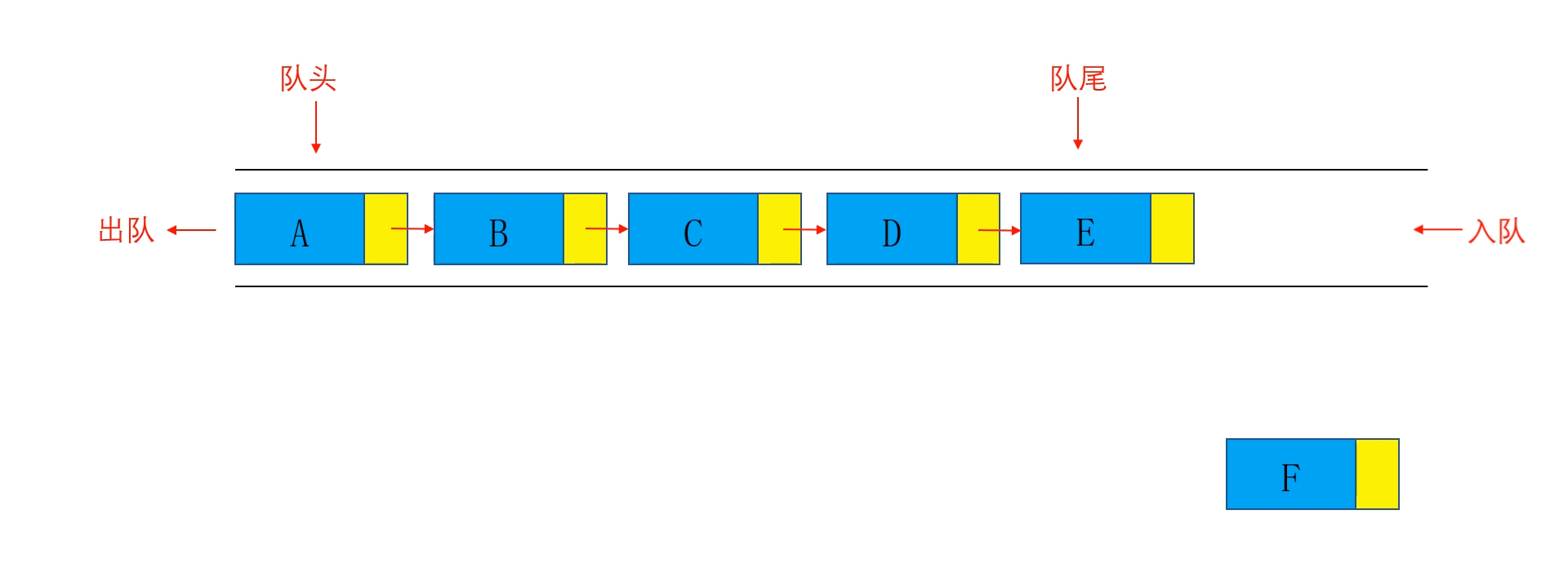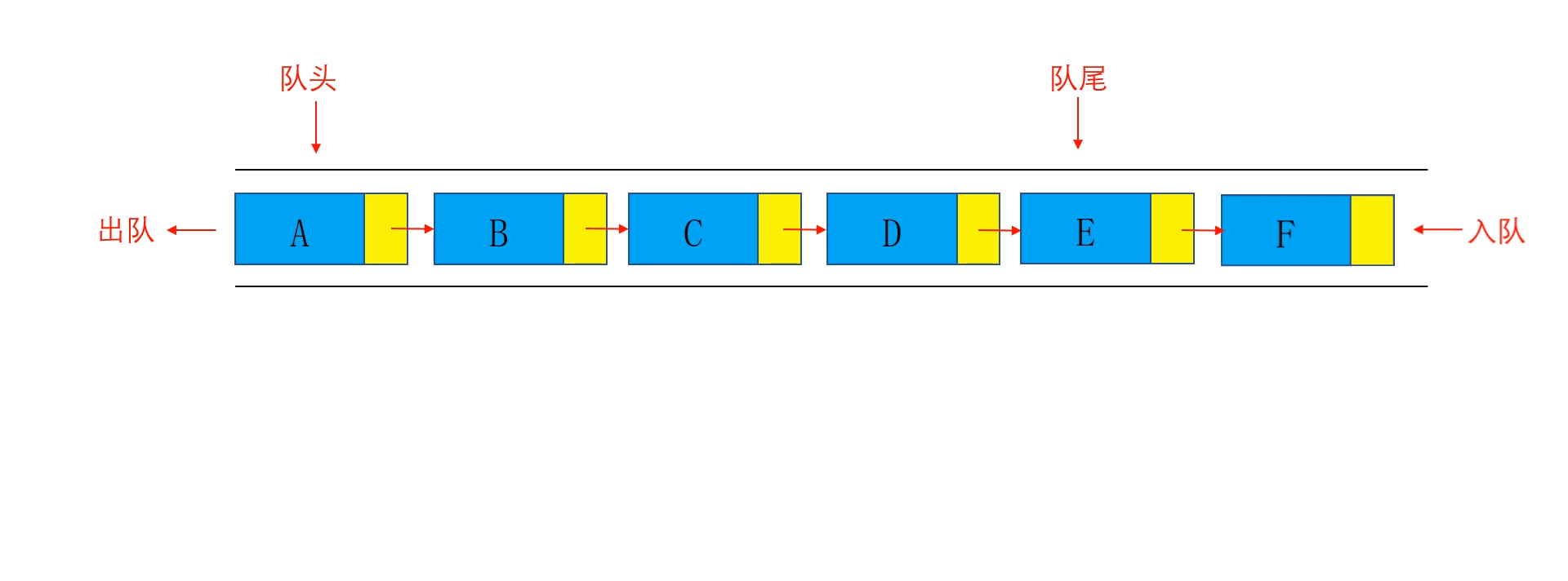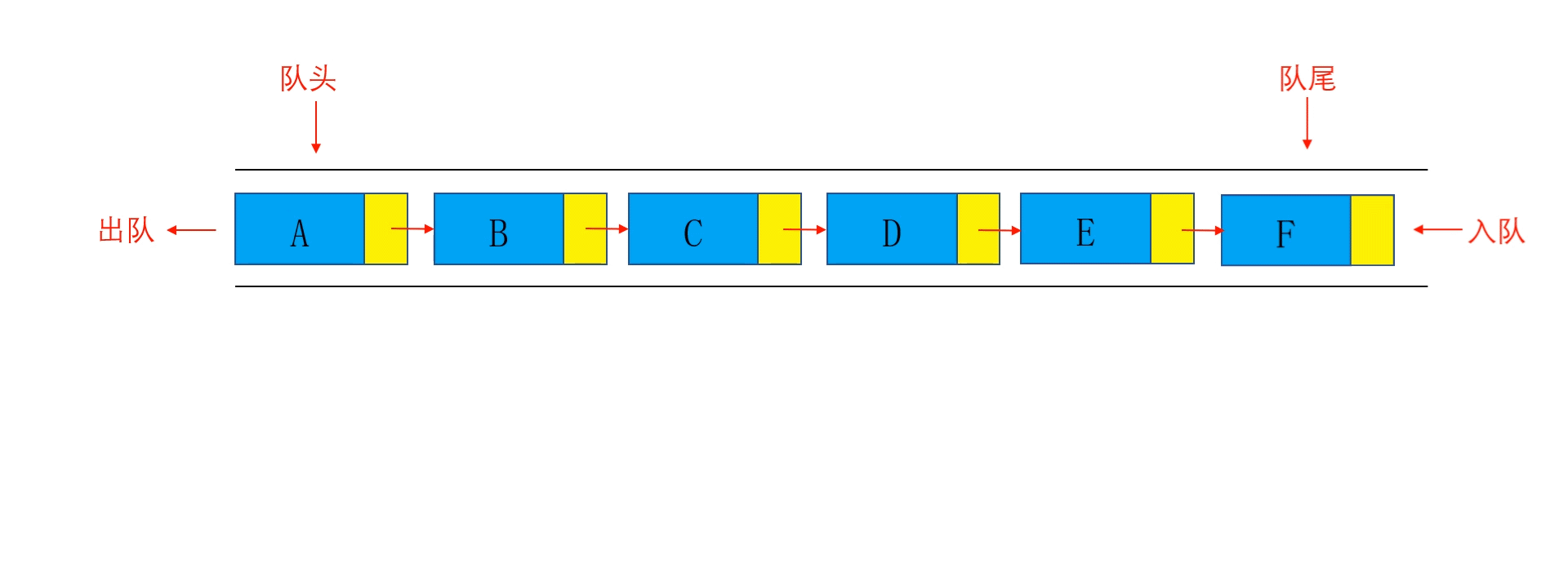
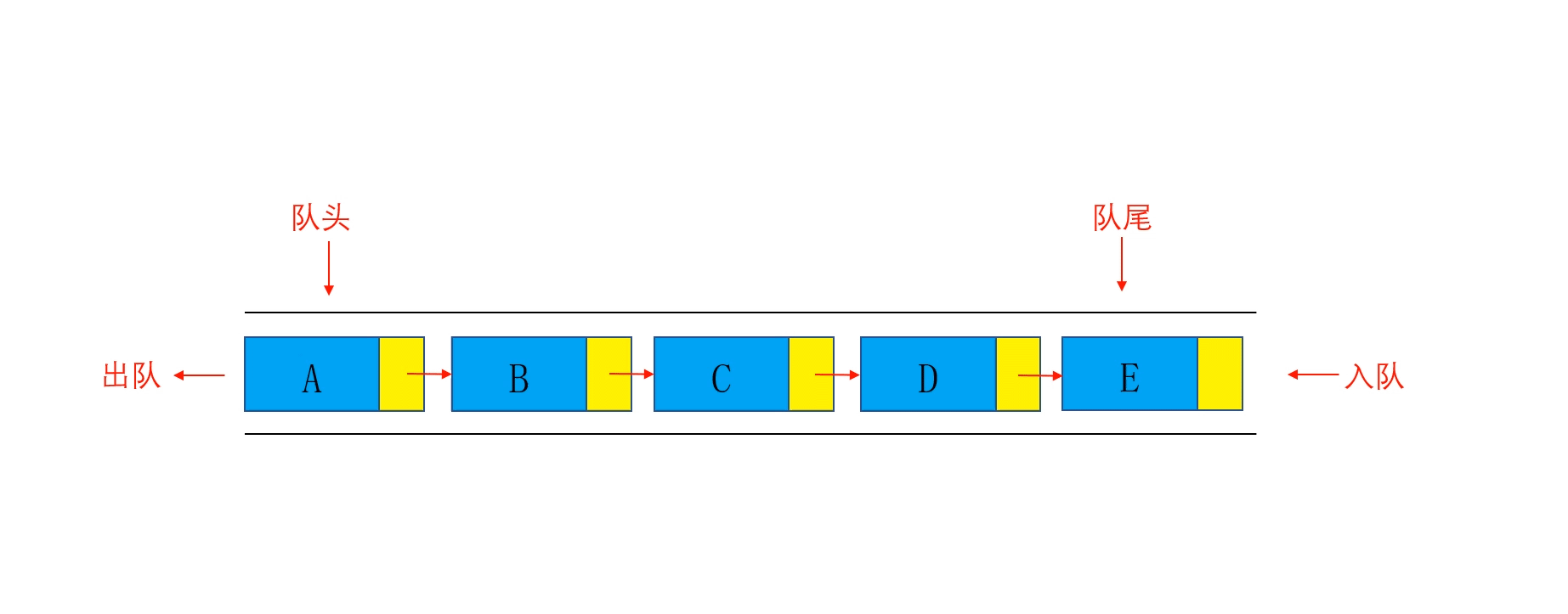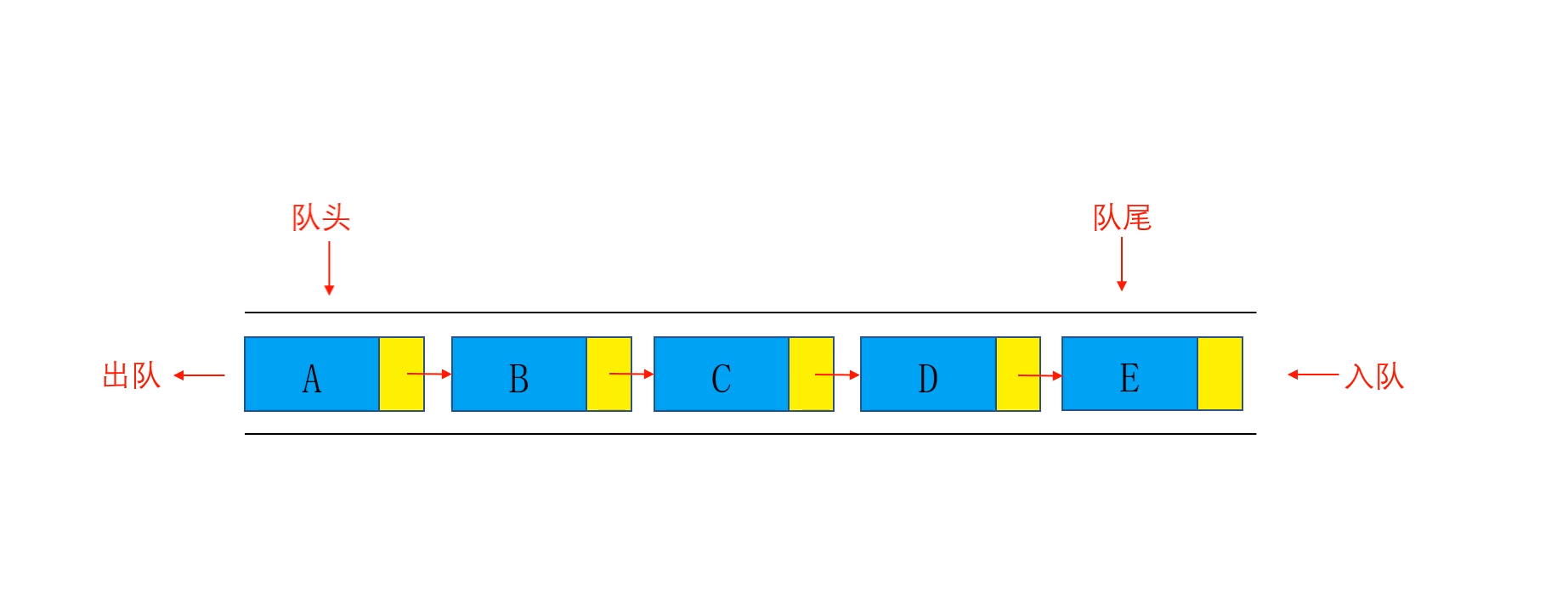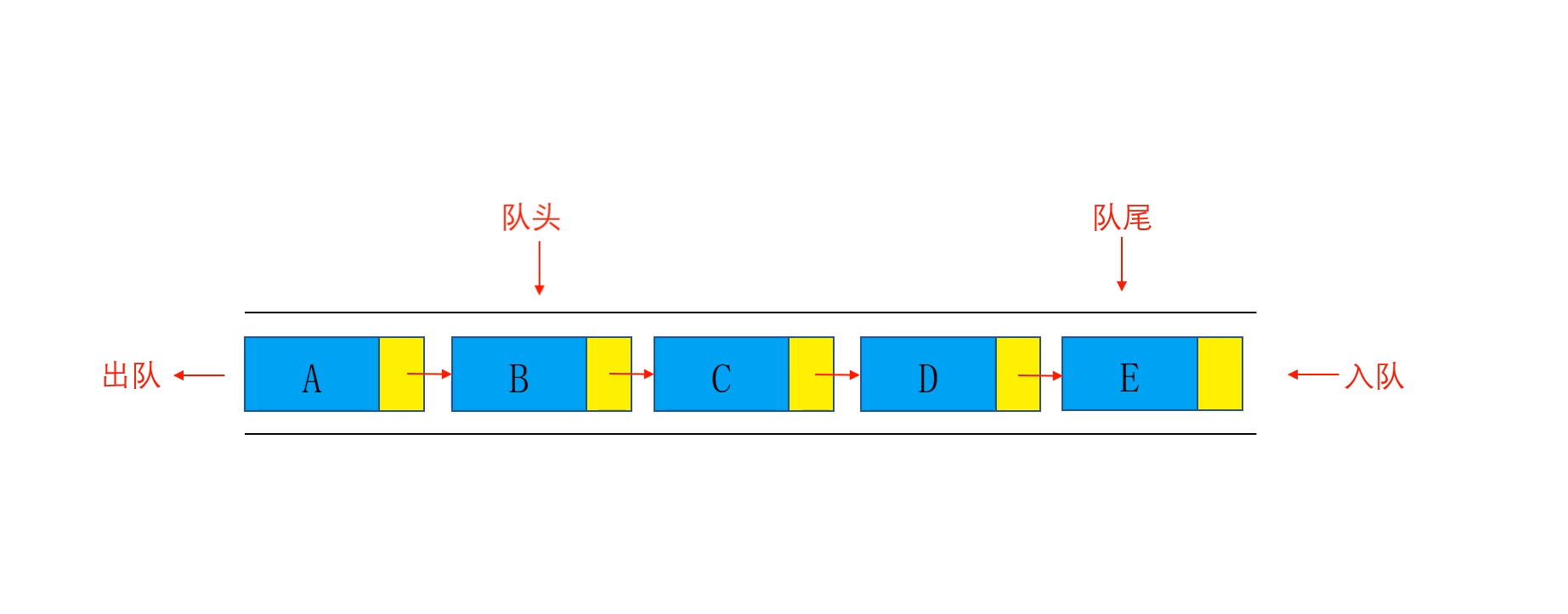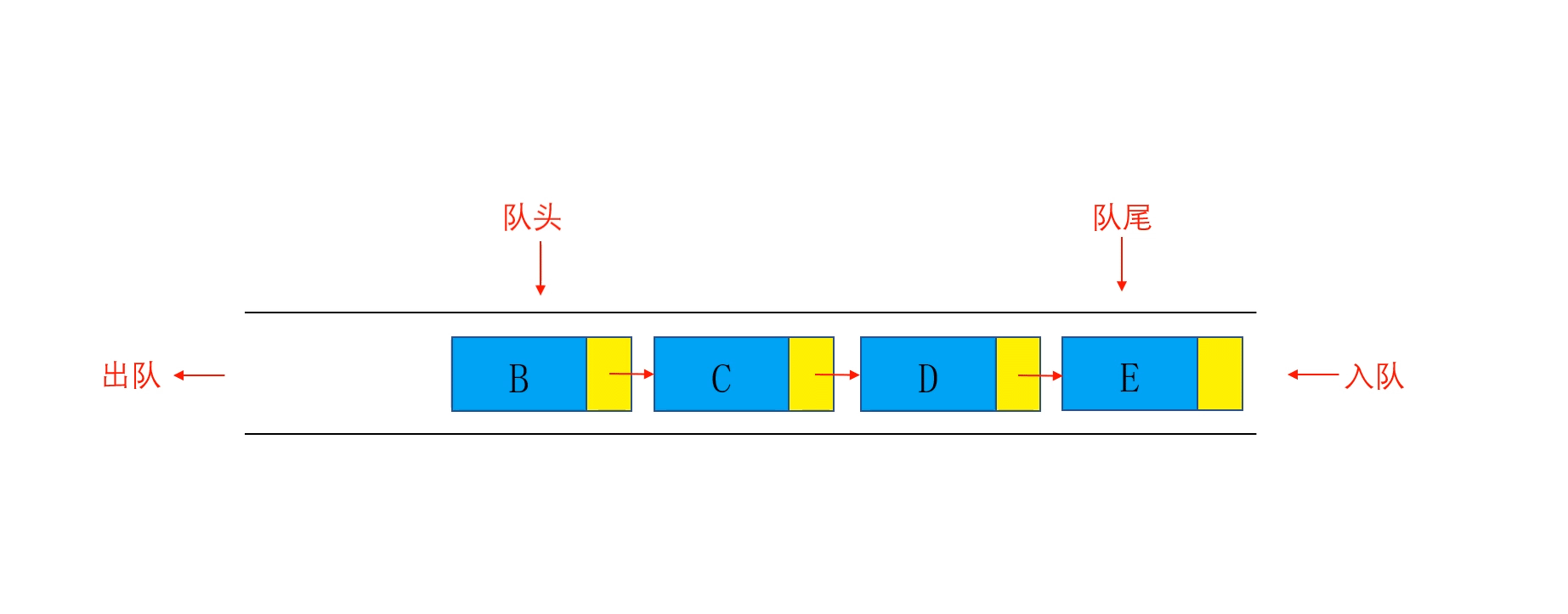
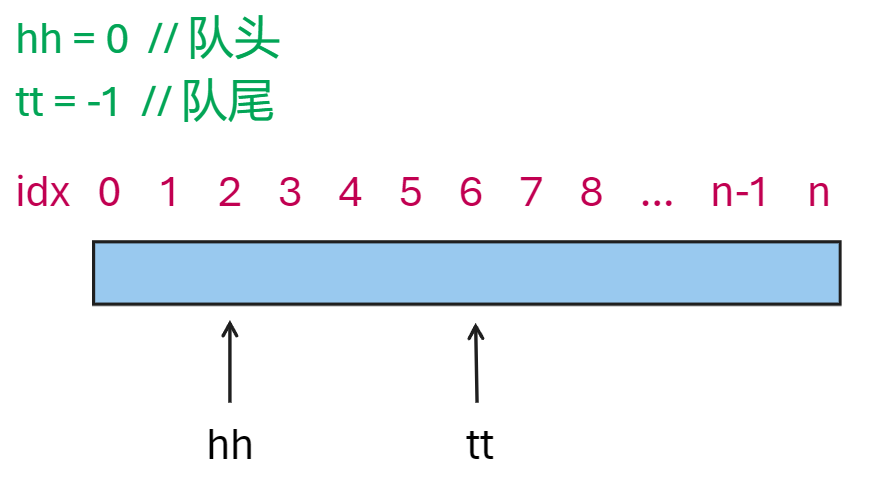
数组模拟队列

//普通队列
int q[N], hh = 0, tt = -1; //hh表示队头，tt表示队尾

//入队
q[++tt] = x;

//出队
hh++;

//返回队首的值
q[hh];

//返回队尾的值
q[tt];

//判断队列是否为空
if(hh <= tt) //非空
else ;//空

//得到队列的长度
tt-hh+1;

STL queue

#include<queue>
queue<int> q;
q.push(x);  // 队尾插入x
q.pop();    // 弹出队头
q.front();  // 查看队头
q.back();   // 查看队尾
q.size();   // 查看q元素个数
q.empty();  // 查看q是否为空

例题：模拟队列

题目描述

实现一个队列，队列初始为空，支持四种操作：

push x – 向队尾插入一个数 x；
pop – 从队头弹出一个数；
empty – 判断队列是否为空；
query – 查询队头元素。

现在要对队列进行 $M$ 个操作，其中的每个操作 $3$ 和操作 $4$ 都要输出相应的结果。

输入格式

第一行包含整数 $M$ ，表示操作次数。

接下来 $M$ 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

数据范围： $1 \leq M \leq 100000$ ， $1 \leq x \leq 10^{9}$ ，所有操作保证合法。

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值

输入样例

10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6

输出样例

NO
6
YES
4

题目分析

数组模拟队列模板题

示例代码

#include <iostream>
using namespace std;
const int N = 100010;

int m;
int q[N], hh, tt = -1;

int main() {
    cin >> m;
    while (m--) {
        string op;
        int x;
        cin >> op;
        if (op == "push") {
            cin >> x;
            q[ ++ tt] = x;
        }
        else if (op == "pop") hh ++ ;
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }
    return 0;
}