KMP匹配算法与Trie树

KMP匹配算法

引言

先来看一个题目：

题目描述

给定一个字符串 $s (1 \leq s . s i z e () \leq 10^{5})$ 和字符串 $p (1 \leq p . s i z e () \leq 10^{4}$ )，所有字符串只包含大小写英文字母和阿拉伯数字。 $P$ 在 $S$ 中多次作为子串出现，请求出 $P$ 在 $S$ 中所有出现位置的起始下标。

输入格式

第一行输入一个正整数 $n$ ，表示字符串 $s$ 的长度。

第二行输入字符串 $s$ 。

第三行输入一个正整数 $m$ ，表示字符串 $p$ 的长度。

第四行输入字符串 $p$ 。

$1 \leq n \leq 10^{5}; 1 \leq m \leq 10^{4}$

输出格式

共一行，输出所有出现位置的起始下标（下标从 $0$ 开始计数），整数之间用空格隔开。

输入样例

5
ababa
3
aba

输出样例

0 2

题目分析

首先容易想到的是 $O (n \times m)$ 的朴素做法：枚举字符串 $s$ 的每个位置 $i$ ，依次比较 $p [0]$ 和 $s [i]$ ， $p [1]$ 和 $s [i + 1]$ ... 是否相等。

但显然，这个做法对于该题的数据范围是会超时的，那上面这个做法有什么地方是冗余的、可以想办法省略的呢？

假设现在给了我们两个字符串，s="ababababfab"，p="ababf"，来看下图的比较流程：

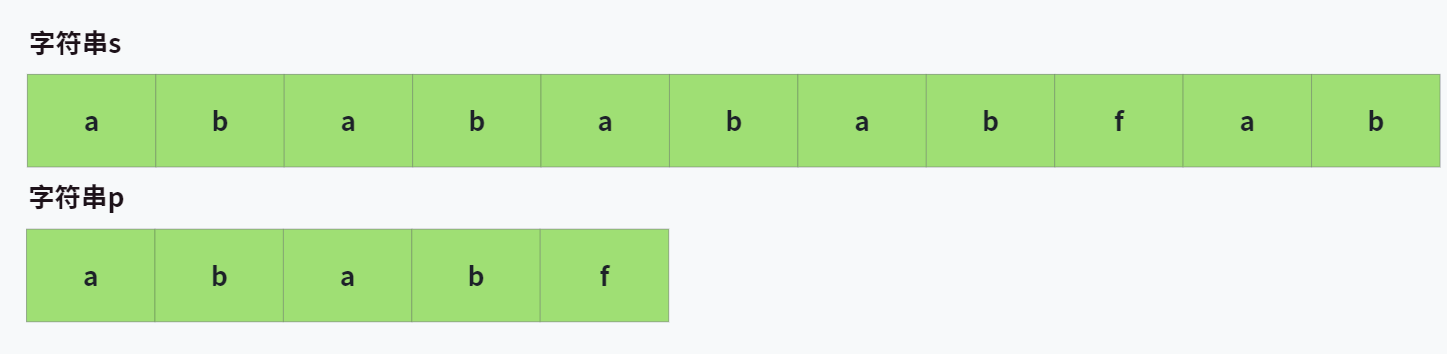
在进行比较时，先从 s[0] 开始，显然第一轮比较的是 ababa 和 ababf ，在最后一个字符处匹配失败了。

紧接着我们会从 s[1] 开始，比较 babab 和 ababf 。

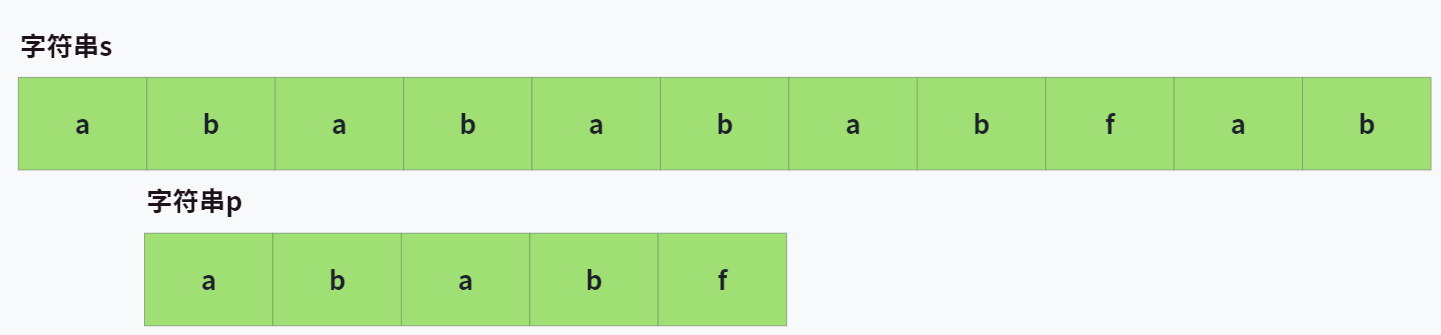
显然是不相同的，所以接着往后比较，直到遇到某个地方完全相同为止。发现了吗，在这个操作流程中，有哪些时候我们可以省略不去匹配呢？

让我们回到第一次匹配的时候，当走到 s[4] 和 p[4] 时，实际上得到了如下的信息：

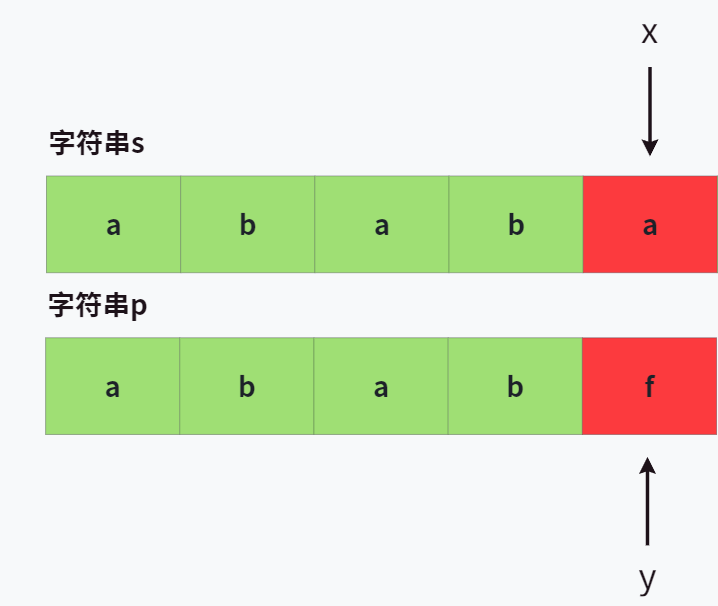
image.png|325

从我们上帝视角来看，把 p 移到哪个地方开始匹配是 效率高 并且 保证不会有遗漏的地方 的？很明显，应该移到 s[2] 这个位置！

从感性上，很好理解为什么要这样移动，这个一眼就能看出来，但是从程序的角度出发，如何理性的分析处要进行这样的移动呢？

首先，假设我们已经通过 “某种手段” 得知了字符串 p[0, 3] 中，前后相等的最大范围是 p[0, 1] 和 p[2, 3]，那么当 p[0, 3] 和 s[0, 3]全部比较成功，而 p[4] 和 s[4] 比较失败时，现在我们得到的信息有：

p[0, 3] 和 s[0, 3] 是相同的。
p[0, 1] 和 p[2, 3] 是相同的。
字符串 p[0, 3] 中，前后相等的最大范围是 p[0, 1] 和 p[2, 3]。

根据上述信息，可以推出两个结论：

s[0, 1] 和 s[2, 3] 是相同的。
p[0, 1] 和 s[2, 3] 是相同的。

所以，下次从 p[0] 和 s[2] 开始比较时，我们可以略过前两个字符，直接从第三个开始，如下图所示。

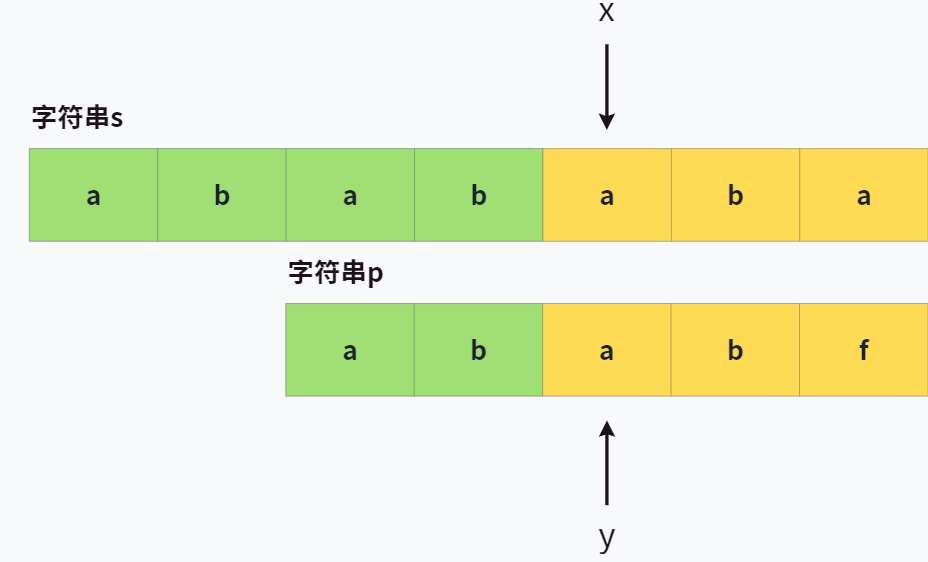
image.png|500

你可能会有这样的问题，为什么 p[0, 1] 不用比了呢？请看结论 $2$ ，因为它们已经相同了。

另一个问题，这样比较之后，就相当于是直接从 s[2] 的位置进行比较了，忽略了 s[1] 开头的情况，是否有影响呢？

答案是没有影响，因为如果代码会从 s[1] 开头进行比较，说明对于 p[0~3] ，它的最长公共前后缀的前缀应该是 p[0~2]，而我们已经知道了最长公共前后缀是 p[0~1] ，所以结果不成立。

可能还会有一个问题，为什么不直接从 p[3] 和 s[5] 比较，aba 是相同的呀？因为上面得到的信息中，并没有 p[2] 和 s[4] 相等这个信息！

OK，让我们按这个规则来继续往后匹配，显然上面那段匹配走到 s[6] 和 p[4] 时又会匹配失败，那么，下次我们应该从哪里开始匹配呢？

image.png|500

是从 p[2] 和 s[6] 开始匹配！你答对了吗？所以，得到了这样的图：

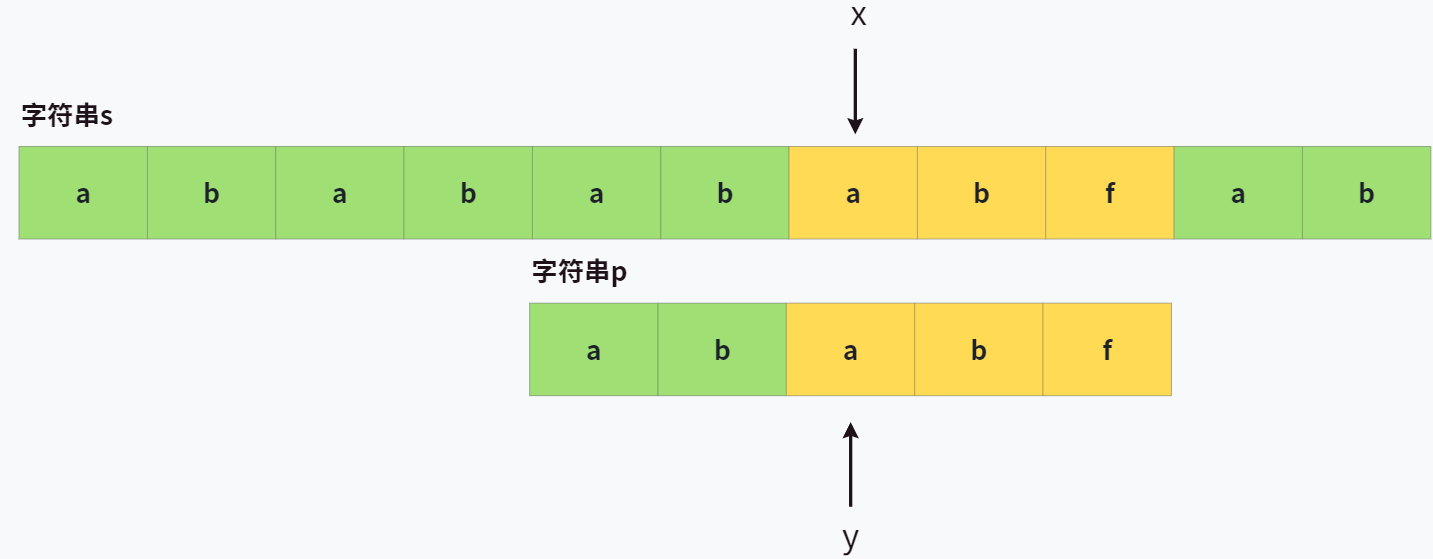
再之后，就匹配成功了~ 发现了吗，在这个过程中，咱们跳过了什么？

跳过了已经匹配成功的前缀，比如 p[0] 和 p[1] 跳过不用比了，直接从 p[2] 开始，这意味着，字符串 s 的指针 x 是不用回头去重新比较的，而是一直在往前移动。

上述流程，便是 KMP 算法的基本思想，下面我们来正式了解它。

基本概念

KMP算法（Knuth-Morris-Pratt算法）是一种用于在一个文本串（主串）中查找一个模式串（子串）的高效字符串匹配算法。KMP算法的核心思想是利用已经部分匹配的信息，避免不必要的回溯，从而提高匹配的效率。

KMP算法主要包括两个步骤：

构建部分匹配表 next，其中 next[i] 表示对于字符串 p，p[0, i] 这个子串中的最长公共前后缀里，前缀的结束位置。可以理解为，对于 p[0, i]，p[0, next[i]] 和 p[i-next[i], i] 是相等的。
利用 next 表进行匹配。

前置知识

子串：一个字符串 $S$ 中任意连续的字符组成的字符串 $S^{'}$ 称为该字符串的子串

前缀：包含首位字符但不包含末位字符的子串

后缀：包含末尾字符但不包含首位字符的子串

具体实现

上面说到，KMP算法主要就两个步骤，先来看第一个步骤，如何构建 next 表。

求 next 表

首先重申 next 表的含义，next[i] 代表对于字符串 p，p[0, i] 这个子串中的最长公共前后缀里，前缀的结束位置。可以理解为，对于 p[0, i]，p[0, next[i]] 和 p[i-next[i], i] 是相等的。

来看一个实例：

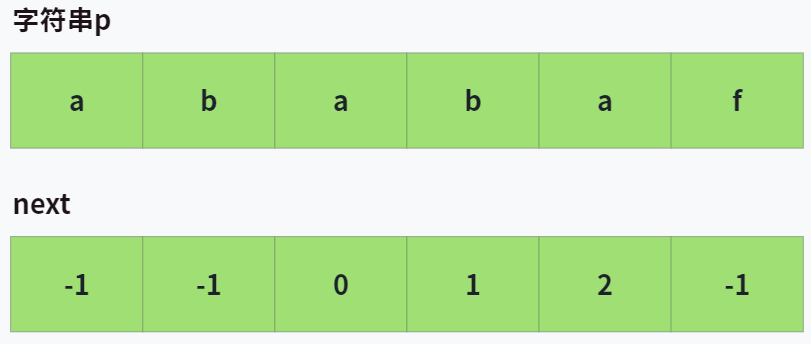
image.png|500

其中 -1 表示没有匹配的，不多赘述，我们来看另外几个不是 -1 的。

为什么 next[2] 是 0 呢？因为在 p[0, 2] 这一段中，最大匹配的前后缀是 p[0, 0] 和 p[2, 2] 。
为什么 next[3] 是 1 呢？因为在 p[0, 3] 这一段中，最大匹配的前后缀是 p[0, 1] 和 p[2, 3] 。
为什么 next[4] 是 2 呢？因为在 p[0, 4] 这一段中，最大匹配的前后缀是 p[0, 2] 和 p[2, 4] 。

相信基本含义你已经明白了，那接下来的重点就在于如何求出 next 表呢？好了，把你要说的 “暴力” 两个字收回去，如果暴力两层循环又变成了 $O (n^{2})$ 的时间复杂度，那就没必要了。

我们来做一个预设，在求 next[i] 的时候，前面的 next[0, i-1] 已经求出来了，那如何利用这些信息来求 next[i] 呢？

为了方便看，我们设 j = next[i-1] ，可以把 j 理解为 已匹配的前缀字符串的最后一位 。这说明 p[0, j] 和 p[i-1-j, i-1] 是匹配的。

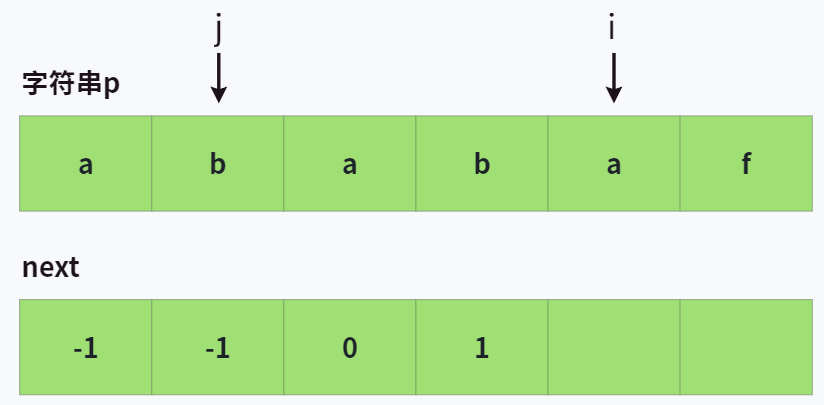
那对于 next[i] ，我们要怎么去求呢？从贪心的角度来说，首先我们会希望这个长度能更长，根据 j 给我们的信息，我们知道，如果 p[j+1] == p[i]，那么说明 p[0, j+1] 和 p[i-j-1, i] 是匹配的，那此时对于 p[0, i] ，其最长公共前后缀的前缀就是 p[0, j+1]，所以 next[i] = j+1 。

为什么？首先 p[0, j+1] 和 p[i-1-j, i] 匹配的原因应该不必赘述，但为什么一定不会有更长的公共前后缀呢？

假设有，就假设 p[0, j+2] 和 p[i-j-2, i] 是匹配的吧，这里面就隐含一个信息，p[0,j+1] 和 p[i-j-2,i-1] 匹配，那这样的话，next[i-1] 的值就应该是 j+1，而不是 j 了，所以明显具备冲突，不成立。

所以得到结论，当 p[j+1] == p[i] 时，那么 p[0, j+1] 必然就是 p[0, i] 的最长公共前后缀，即 next[i] = j+1 。

OK，那么让我们再来看第二种情况，如果 p[j+1] != p[i] 呢？

在处理这一段时，先重申一遍，next[i] 代表对于字符串 p，p[0, i] 这个子串中的最长公共前后缀里，前缀的结束位置。可以理解为，对于 p[0, i]，p[0, next[i]] 和 p[i-next[i], i] 是相等的。

来看一个实例：

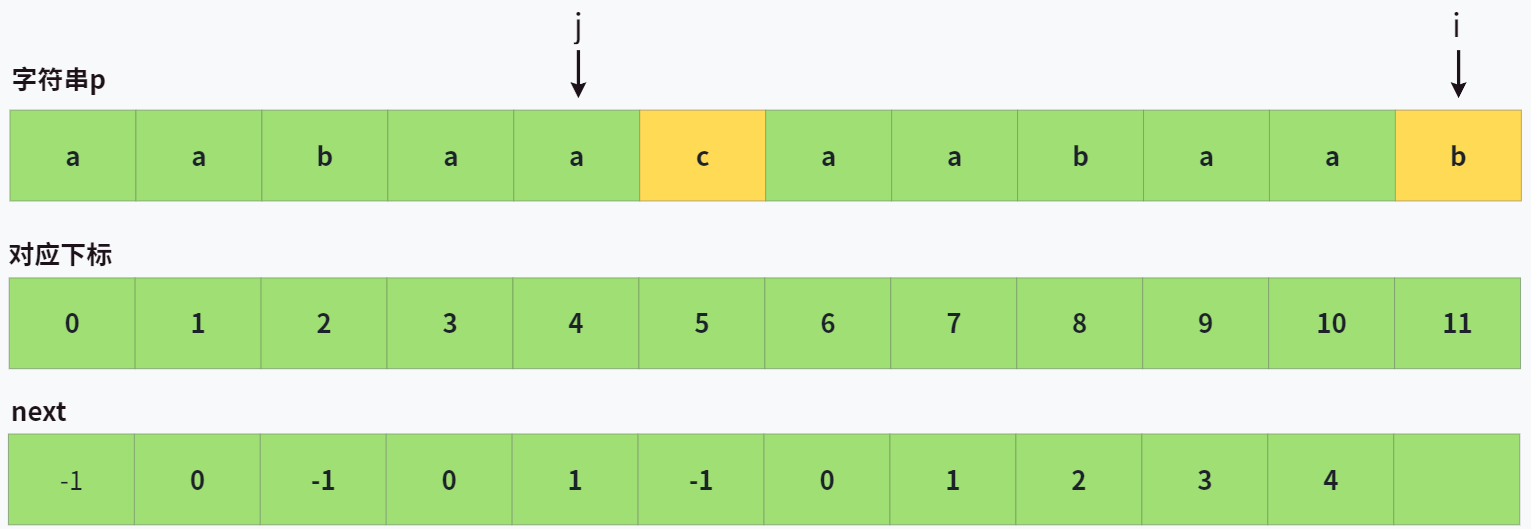
对于上图，j=4, i=11，显然 p[j+1] != p[i]，所以 next[i] 也不等于 j+1 ，但这时 p[i] 要和谁去匹配呢？

因为 p[0, j] 和 p[i-j-1, i-1] 是匹配的，再假设 k = next[j]，那么有：

p[0, k] 和 p[j-k, j] 是匹配的。
p[0, j] 和 p[i-1-j, i-1] 是匹配的。

标粉(还是紫)色代表这几段是相等的。

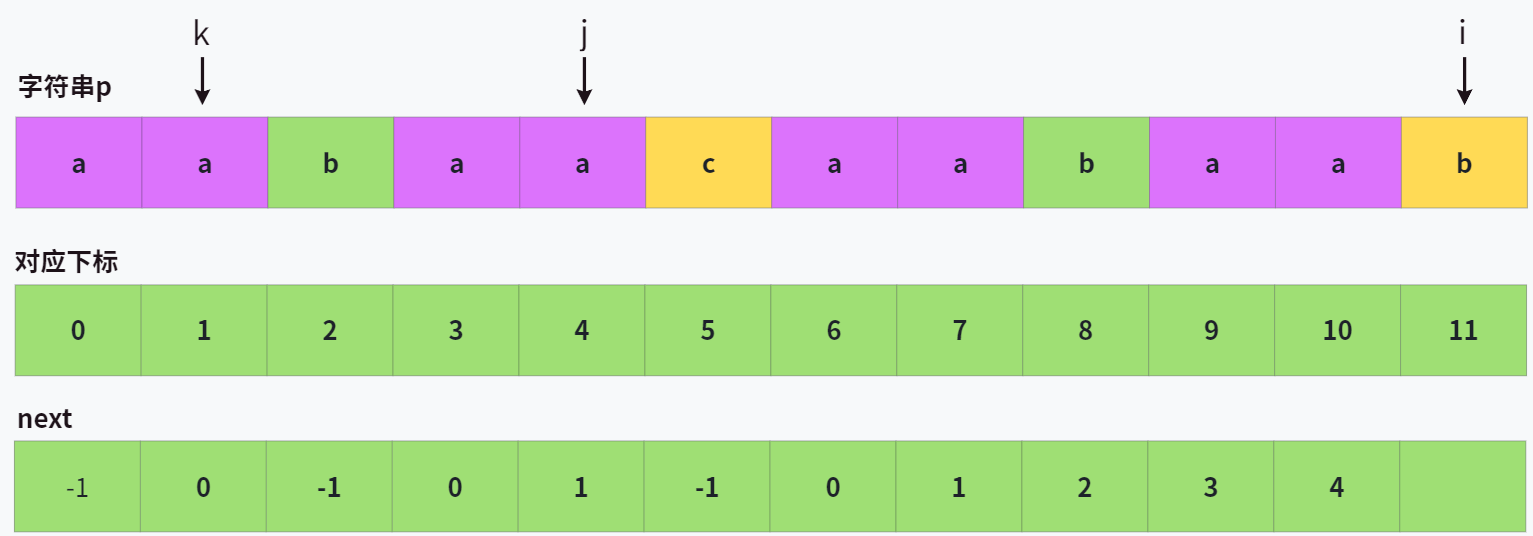
可以得出：p[0, k] 和 p[i-1-k, i-1] 是匹配的。所以，有没有可能 p[k+1] == p[i] 呢？如果有的话，那么 next[i] 就等于 k+1 ！

而假如 p[k+1] != p[i] 呢？那就再去 p[0, next[k]] 看看！所以显然，我们会不断循环重复这个步骤，直到某一次得到了结果或者 k 取到的值是 -1 ，就结束了，取到 -1 说明没有公共前后缀，那就只判断 p[0] 和 p[i] 即可。

至于为什么不会有更长的呢？证明方式和前面是一样的，就不重复了。

所以，得出结论，当 p[j+1] != p[i] 时，可以让 j = next[j] ，然后再判断 p[j+1] 是否等于 p[i] ，不断重复该步骤，直到 j == -1 或者 p[j+1] == p[i] 为止。

总结

令 j = next[i-1]，有两种情况：

情况1：p[j+1] == p[i]，那么 next[i] 的值就是 j+1 。

情况2：p[j+1] != p[i]，那么让 j = next[j]，再次判断是否满足情况1。

示例代码如下：

nxt[0] = -1;  
for (int i=1, j=-1; i<n; i++) {  
	while (j != -1 and p[i] != p[j+1]) j = nxt[j];  // 情况2
	if (p[i] == p[j+1]) j++;  // 这样写是为了方便处理p[0]和p[i]不相等的情况。
	nxt[i] = j;  
}

求结果

我们依旧假设 next[i-1] 的值是 j，那么现在要匹配的就是 s[i] 和 p[j+1] ，会发生两种情况：

s[i] == p[j+1] 时，继续匹配下一位即可，而如果全匹配了，那么表示找到了子串。
s[i] != p[j+1] 时，此时暴力解法为重新从 p[0] 开始匹配，所以慢。而 KMP 的做法则是根据所求的 next 表，看看能否和前缀那块匹配上，原理很像求 next 表的操作二。

示例代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5;

int n, m;
string s, p;
int nxt[N];  // nxt[i] 表示 p[0~i] 字符串中，最长公共前后缀的前缀结束位置

int main() {
	cin >> m >> s >> n >> p;
	
	nxt[0] = -1;
	int j = -1;  // j表示上一次匹配的结果
	
	for (int i=1; i<n; i++) {
		while (j != -1 and p[i] != p[j+1]) j = nxt[j];
		if (p[i] == p[j+1]) j++;
		nxt[i] = j;
	}
	
	j = -1;  // j表示p字符串中已匹配字符串的下标
	for (int i=0; i<m; i++) {
		while (j != -1 and s[i] != p[j+1]) j = nxt[j];
		if (s[i] == p[j+1]) j++;
		if (j == n-1) {
			cout << i-n+1 << " ";
		}
	}
	return 0;
}

Trie 树

Trie树又叫字典树，或者单词查找树，是一种用于在字符串集合中高效存储和查找字符串的树形数据结构。

应用

维护一个字符串集合，支持两种操作：

向集合中插入一个字符串string
询问一个字符串string在集合中出现了多少次

原理

一颗空的 Trie 树仅包含一个根节点，该点的字符指针指向空。

而非空的 Trie 树具备以下性质：

根节点为空，其他节点都代表一个字符。
从根节点到某一节点经过的字符，连接起来构成一个字符串，比如下图中的 aced 。
一个字符串和 Trie 树中的一条路径对应。
另外，对于每个节点，会有一个标志，来标记该节点是否是一个字符串的结尾，这里用※来表示。

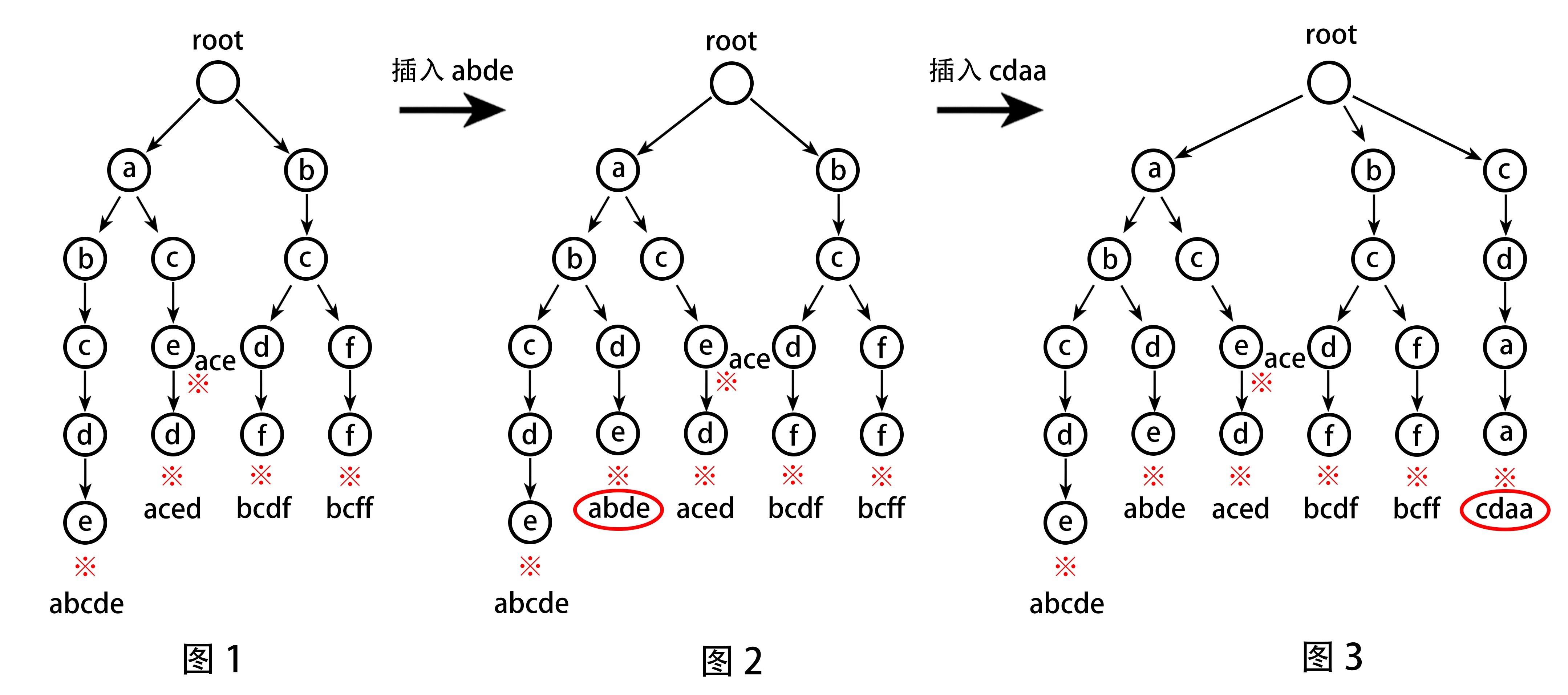
下面是一棵 Trie 树的示例：

图1：原字符串集合：{abcde, ace, aced, bcdf, bcff}

图2：插入字符串：{aced, cdaa}

图3：新字符串集合：{abcde, ace, aced, bcdf, bcff,aced, cdaa}

※ 为字符串结束的标记。

trie树1 2.jpg

Trie树一般具备两种操作：

插入操作 insert

插入操作要实现的功能，就是把一个字符串插入到 Trie 树中。

插入的过程可以这样理解：

如果当前节点已经存在，则继续往下找。
如果当前节点不存在，则建一个新的节点，继续往下。
当走到终点时，标记当前节点是一个终点。

转为实际代码流程，当需要插入字符串 S 时，令一个指针 P 表示 上一个完成插入的节点，显然最开始的时候 P 应该指向根节点。

然后依次扫描字符串 S 的每个字符 ch，按照如下规则进行：

若 P 的子节点中存在字符是 ch 的节点 Q，则令 P = Q。
若 P 的子节点中不存在字符是 ch 的节点，则新建一个节点 Q，令 P 的 ch 字符指针指向Q，再令 P = Q。

当 S 中的字符扫描完毕时，在当前节点 P 上标记它是一个字符串的结尾。

查询查找 query

查询操作要实现的功能，是查询一个字符串在 Trie 树中是否存在，或者是出现的次数，流程和插入的过程很像。

当需要查询字符串 S 时，令一个指针 P 表示 上一个查询的节点，显然最开始的时候 P 应该指向根节点。

然后依次扫描字符串 S 的每个字符 ch，按照如下规则进行：

若 P 的子节点中不存在字符是 ch 的节点，表示字符串 S 没有出现过，结束查询。
若 P 的子节点中存在字符是 ch 的节点 Q，则令 P = Q。

当S中的字符扫描完毕时，若当前节点 P 被标记为一个字符串的结尾，则说明 S 存在于Trie中，否则说明 S 不存在于Trie中。

例题：Trie字符串统计

题目描述

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。

共有 $N$ 个操作，所有输入的字符串总长度不超过 $10^{5}$ ，字符串仅包含小写英文字母。

输入格式

第一行包含整数 $N$ ，表示操作数。

接下来 $N$ 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

数据范围： $1 \leq N \leq 2 * 10^{4}$

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。每个结果占一行。

输入样例

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例

1
0
1

题目分析

Trie树模板题，代码实现的要点：

son[N][x] 表示的含义：

$N$ 是题目给定的数据范围，对于此题，表示字符串的总长度。

$x$ 表示儿子节点的可能性有多少，本题字符串均为小写字母，所以为 $26$ 。

而 son[i][j] 中的值，代表 i 号节点的字符为 j 的儿子节点的编号是 son[i][j] ；如果为 $0$ ，则表示 i 号节点没有字符为 j 的儿子节点。

idx 的含义：

类似于链表中的 idx。由于是用数组来模拟类似链表的节点，所以需要一个变量来辅助我们，idx就是这个辅助变量，它表示当前可以用的节点是哪一个。

示例代码

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int son[N][26], cnt[N], idx; // idx为当前用到的节点，son[i][j]为当前节点的儿子节点，cnt[i]统计以节点i结尾的单词有多少个 

void insert(string str) // 插入新串
{
    int p = 0;
    for (int i = 0; i < str.size(); i ++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx; // 建新节点
        p = son[p][u];
    }
    cnt[p] ++ ;
}

int query(string str)  // 查找
{
    int p = 0;
    for (int i = 0; i < str.size(); i ++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main() {
    int n;
    cin >> n;
    while (n -- ) {
        char op;
        string str;
        cin >> op >> str;
        if (op == 'I') insert(str);
        else cout << query(str) << endl;
    }

    return 0;
}

例题：最大异或对

题目描述

在给定的 $N$ 个整数 $A_{1} ， A_{2} \dots \dots A_{N}$ 中选出两个进行 $x o r$ （异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 $N$ 。

第二行输入 $N$ 个整数 $A_{1} ～ A_{N}$ 。

数据范围： $1 \leq N \leq 10^{5}, 0 \leq A i < 2^{31}$

输出格式

输出一个整数表示答案。

输入样例

3
1 2 3

输出样例

题目分析

很容易想到暴力做法，外层循环 i 枚举所有数，内层寻找与当前 i 异或最大的数，维护一个异或最大值。时间复杂度 $O (N^{2})$ ，显然结果为TLE。

优化：

对于外层枚举的每个数 $a_{i}$ ，如果能以 $O (l o g n)$ 的时间复杂度找到与它异或最大的数 $a_{j}$ ，就不会超时了。

从贪心的角度想，若想要异或的结果尽可能大，那么两个数的异或位要尽可能多，并且越高位的异或越重要。

所以我们要做的事，就是查找数字 a 对应的最多位异或数字是谁，并在这个过程中算出异或的结果。

可以借助Trie树数据结构来完成：将每个数以32位二进制的形式存入Trie树，不够32位则前面补零，查找的时候从最高位查询有无该位的相反异或位。

示例代码

#include <bits/stdc++.h>   
using namespace std;  
/*  
查找每个数字的最大异或值，即尽可能每一位都相反。  
而且是要从最高位进行比较，所以存储的时候也要从最高位开始存储  
*/  
  
const int N = 1e5+5, M = N*31;  
  
int son[M][2], a[N], idx;  
  
void insert(int x) {  
    int p = 0;  // 从根节点开始遍历  
    for (int i=30; i>=0; i--) {  // x >> i & 1，就是取i+1位  
        int u = (x >> i) & 1;  
        if (!son[p][u]) son[p][u] = ++idx;  
        p = son[p][u];  
    }  
}  
  
int find(int x) {  
    // 查找x的最大异或值  
    int p = 0, sum = 0;  
    for (int i=30; i>=0; i--) {  
        // 算出当前的位
        int u = (x >> i) & 1;
        // 先找与它相反的是否存在
        if (son[p][!u]) sum += (1 << i), p = son[p][!u];  
        else p = son[p][u];  
    }  
    return sum;  
}  
  
  
int main() {  
    int n;  
    cin >> n;  
    for (int i=1; i<=n; i++) {  
        cin >> a[i];  
        insert(a[i]);  
    }  
    int res = 0;  
    for (int i=1; i<=n; i++) {  
        res = max(res, find(a[i]));  
    }  
    cout << res;  
    return 0;  
}