双指针

基本概念

双指针算法是一种入门级算法，这里的指针并不是C语言里面用来保存地址的指针，而是用来遍历扫描序列或者数组的下标，可以简单理解为循环变量 $i$ 或 $j$。

双指针算法可以分为两大类别：
第一类：两个指针指向同一序列，如冒泡、选择、插入等排序算法其实都是双指针。
第二类：两个指针分别指向不同序列，如归并排序的归并过程。

按特点可以划分为：左右指针（碰撞指针）、快慢指针（滑动窗口）。

基本上所有的双指针问题都是由暴力优化而来，所以我们可以从暴力解法入手，再去思考如何优化，可以优化的问题一般都会满足某种性质，如单调性。双指针可以将原本 $O(n^2)$ 级别时间复杂度优化到 $O(n)$ 级别。

例题精讲

例题：盛最多水的容器

题目描述

给定一个长度为 $n(2\le n\le {10}^5)$ 的整数数组 $h(0\le h_i\le {10}^4)$ 。有 $n$ 条垂线，第 $i$ 条线的两个端点是 $(i,0)$ 和 $(i,h_i)$ 。找出其中的两条线，使得它们与 $x$ 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量 $m$。

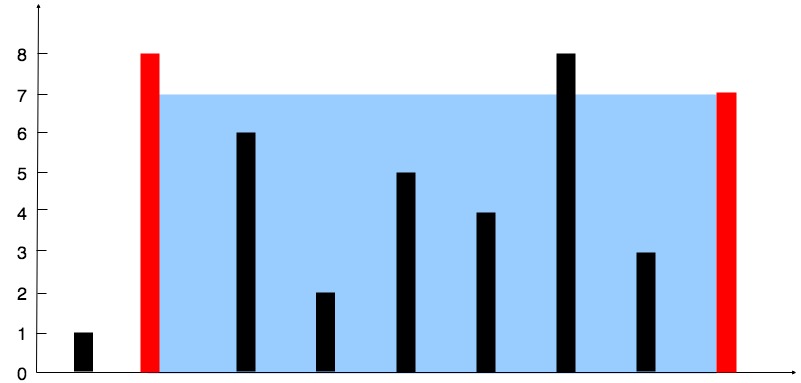
输入格式

第一行输入一个正整数 $n$。

第二行输入 $n$ 个正整数 $h_i$。

输出格式

输出最大水量 $m$

输入样例

9
1 8 6 2 5 4 8 3 7

输出样例

49

题目分析

任意两根不同的垂线都可以围成一个储水槽，可以很容易想到枚举所有可能的情况，取一个最大盛水量即为答案，核心代码如下：

int solve() {
    int ans = 0;
    for (int i = 1; i <= n; i++)
        for (int j = i+1; j <= n; j++) {
            int w = min(h[i], h[j]) * (j-i);
            ans = max(ans, w);
        }
    return ans;
}

上面的代码，时间复杂度是$O(n^2)$，题中 $n$ 的范围取到 ${10}^5$，此种做法会严重超时，我们得在暴力做法的基础上，想办法进行优化。

首先这个问题最终其实是要确定一个子区间，使得子区间围起来的面积最大。

那不妨在最开始先让 $i$ 指针指向最左端点 $1$，$j$ 指针指向最右端点 $n$，并得到了第一个可能的答案：min(h[1], h[n])*(n-1) 。

那么下面，就要考虑把 $i$ 指针右移还是 $j$ 指针左移了。可以发现，不管是谁移动，底边的长度是一样的，也就是在 min(h[i], h[j]) * (j-i) 这个式子中，不管移动谁，变化后的 (j-i) 的值都是一致的，所以就要让 min(h[i], h[j]) 的值有可能变大。于是要做的事就很显然了，我们应该把 $i$ 和 $j$ 进行比较，谁更小移动谁，这样才可能使结果变大。

那么，针对每次移动，都用这个方案进行决策，必定能在这个过程中找到最大值。

示例代码

int solve() {
    int i = 1, j = n;
    int ans = 0;
    while (i < j) {
        int w = min(h[i], h[j]) * (j-i);
        ans = max(ans, w);
        if (h[i] <= h[j]) i++;
        else j--;
    }
	return ans; 
}

$i、j$ 指针总共移动次数为 $n$ 次，时间复杂度由原来的$O(n^2)$ 降低到了 $O(n)$。

例题：判断子序列

题目描述

给定一个长度为 $n$ 的整数序列 $a_1,a_2,\dots ,a_n$ 以及一个长度为 $m$ 的整数序列 $b_1,b_2,\dots ,b_m$。请你判断 $a$ 序列是否为 $b$ 序列的子序列。

子序列指序列的一部分项按原有次序排列而得的序列，例如序列 $a1,a3,a5$ 是序列 $a1,a2,a3,a4,a5$ 的一个子序列。

输入格式

第一行包含两个整数 $n,m$。

第二行包含 $n$ 个整数，表示 $a1,a2,\dots ,a_n$。

第三行包含 $m$ 个整数，表示 $b1,b2,\dots ,b_m$。

$1\le n\le m\le {10}^5,-{10}^9\le ai,bi\le {10}^9$

输出格式

如果 $a$ 序列是 $b$ 序列的子序列，输出一行 Yes。

否则，输出 No。

输入样例

3 5
1 3 5
1 2 3 4 5

输出样例

Yes

题目分析

子序列可以不必连续，我们可以考虑使用两个指针 $i,j$ 分别指向 $a,b$序列，若 $a[i]==b[j]$，则 $i,j$ 指针均往后移动一位，否则让 $j$ 指针往后移动去找与当前当前 $a[i]$ 匹配的元素。若最后能够匹配，则 $i$ 指针一定能够扫描完整个 $a$ 序列，判断 $i$ 的值即可。

示例代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N], b[N]; 

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < n; i++) cin >> a[i];
	for (int i = 0; i < m; i++) cin >> b[i];
	
	int i = 0, j = 0;
	while (i < n && j < m)
	{
		if (b[j] == a[i]) i++, j++;
		else j++;
	}
	if (i == n) cout << "Yes";
	else cout << "No";
	return 0;
}

例题：数组求和

题目描述

给定两个数组 $a$ 和 $b$，保证数组元素都是非降序的。读入一个正整数 $k$。求出使得 $a[i]+b[j]=k$ 的满足条件的 $i$ 和 $j$。数据保证有唯一的解。

输入格式

第一行，读入三个数 $n,m,k$ —— 表示数组 $a$ 的长度，数组 $b$ 的长度，给定的 $k$ 值。

第二行为 $n$ 个整数，为数组 $a$ 的元素值 。

第三行为 $m$ 个整数，为数组 $b$ 的元素值。

保证数组元素值在 $int$ 范围内，且同一数组元素各不相同。

$1<=n,m<={10}^5$

输出格式

共一行，包含两个整数 $i$ 和 $j$。

输入样例

4 5 10
1 2 3 9
3 4 6 8 12

输出样例

1 3

题目分析

首先很容易想到朴素解法，双重循环分别扫描 a，b 数组的每个元素，求使得 a[i]+b[j]=k 成立的 i 和 j 即可。可以很快得到如下代码

// 朴素解法
for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
        if (a[i] + b[j] == k)
        {
            cout << i << " " << j << endl;
	    	return 0;
		}

上述代码的时间复杂度是 $O(nm)$，而数据范围是 ${10}^5$ 数量级，肯定会超时，此时需要考虑优化，重新读题可以发现给定数组存在单调性——即数组元素是非递减排好序的。

我们可以使用碰撞指针来对上面的朴素算法进行优化，题目求使得a[i] + b[j] == k成立的 i 和 j，那就让 i 从小到大扫描数组 a，j 从大到小扫描数组 b。

那么，假如此刻 a[i]+b[j]>k，那么势必要把 j 左移，总和减少才可能得到答案；

同理，如果此刻 a[i]+b[j]<k，那么势必要把 i 右移，总和增加才可能得到答案。

由于答案一定存在且唯一，所以一定可以找到满足条件的 i 和 j。

示例代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N], b[N]; 

int main()
{
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 0; i < n; i++) cin >> a[i];
	for (int i = 0; i < m; i++) cin >> b[i];
	for(int i = 0, j = m - 1; i < n; i++)
	{
	    while(b[j] + a[i] > k) j--;  // 大于说明符合条件的b[j]在左边
	    
	    if(b[j] + a[i] == k) 
	    {
	        cout << i <<  " " << j << endl;
	        return 0;
	    }
	}
	return 0;
}

上述代码最多扫描整个a数组一遍，b数组一遍，时间复杂度为$O(n+m)$，可以轻松通过。

例题：最长连续不重复子序列

题目描述

给定一个长度为 $n$ 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式

第一行包含整数 n ($1\le n\le {10}^5$)。

第二行包含 $n$ 个整数（均在 $0\sim$${10}^5$ 范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。。

输入样例

5
1 2 2 3 5

输出样例

3

题目分析

首先考虑朴素做法：遍历 $i$ 和 $j$ 的所有情况，对每个 $i$ 和 $j$ 维护的子区间，检查 [i,j]是否满足给定的条件，对答案进行更新。

时间复杂度是$O(n^3)$。代码如下：

const int N = 1e5 + 10;
int a[N];

// 以i结尾的子序列中最长连续不重复长度
for (int i = 0; i < n; i++)
    for (int j = 0; j <= i; j++)
        if (check(j, i) == 0)//检查 i 和 j 之间是否有重复的数字
        	res = max(res, i - j + 1);

优化：上述暴力做法很慢的原因在于 j 指针一直在走回头路，有没有什么办法能让 j 指针不走回头路呢？

外层循环 i 枚举每个字符，假设 a[j]~a[i] 满足当前以 i 为结尾的最长连续不重复子串，当 i 指针往右走时，若进来一个重复的数，我们要如何让 a[j]~a[i] 重新满足连续且不重复的性质呢？答案是让 j 继续往右走，直到将与 a[i+1] 重复的元素去掉，此时以 i+1 为结尾的最长连续不重复子串就得到了更新。

如何知道 a[i+1] 是否重复了？标记 a[j]~a[i] 中的每个数就行了！若 a[i+1] 已经被标记过，说明肯定在a[j]~a[i] 中出现过了。通过优化后，i 最多扫描一遍 n，j 也最多扫描一遍 n，时间复杂度为 $O(n)$。

示例代码

#include<iostream>
using namespace std;

const int N = 1e5 + 10;
int st[N], a[N];

int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) cin >> a[i];
	
	int res = 0;
	for (int i = 0, j = 0; i < n; i++)
	{
		st[a[i]]++;
		while (j < i && st[a[i]] > 1)
		{
			st[a[j]]--;
			j++;
		}
		res = max(res, i-j+1);
	}
	cout << res;
	
	return 0;
}

模板总结

for (int i = 0, j = 0; i < n; i ++ ) {
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}
常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作