二分
二分法是一种在有序序列中查找特定元素的搜索算法,算法的基本思想是将要查找的区间反复地二分为两部分,不断缩小查找范围,直到找到目标为止。
需要注意的是,二分的原理是基于序列有序,若是无序则二分的正确性无法得到保证。
整数集合上的二分
例题:二分模板题
题目描述
给定一个按照升序排列的长度为
输入格式
第一行包含整数
第二行包含
接下来
输出格式
共
如果数组中不存在该元素,则返回
输入样例
6 3
1 2 2 3 3 4
3
4
5
输出样例
3 4
5 5
-1 -1
题目分析
首先可以快速想到的朴素做法是,从头到尾扫描一遍序列,便可以以
题目说给定的序列是有序的,我们能不能利用有序的性质,减少查找的次数从而缩短查找时间呢?
当然可以!由于序列是有序的,我们可以先查找中间值是否等于目标,若不是目标,则比较中间值和目标的大小关系,假设中间值大于目标,由于序列的有序性,中间值后面的值都比目标要大,均可排除,此时我们只需要找中间值前面的值即可。
这样的话,原本需要在
时间复杂度:由于每次都将查找范围缩小一半,所需要的查找比较次数为
下面介绍两个二分查找的算法模板:
模板一:在单调递增序列
bool check1(int mid) {
if (a[mid] >= x) return true;
else return false;
}
int bs1(int l, int r) {
while (l < r) {
int mid = l+r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
模板二:在单调递增序列
bool check2(int mid) {
if (a[mid] <= x) return true;
else return false;
}
int bs2(int l, int r) {
while (l < r) {
int mid = (l+r+1) >> 1; // +1是为了上取整。
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
上述代码中采用 >> 右移运算符来实现除以
示例代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], t;
bool check1(int mid) {
return a[mid] >= t;
}
bool check2(int mid) {
return a[mid] <= t;
}
int bs1(int l, int r) { // 找左边界
while (l < r) {
int mid = l + r >> 1;
if (check1(mid)) r = mid;
else l = mid + 1;
}
return l;
}
int bs2(int l, int r) { // 找右边界
while (l < r) {
int mid = l + r + 1 >> 1; // 向上取整,mid 不能更新为r
if (check2(mid)) l = mid;
else r = mid - 1;
}
return l;
}
int main() {
int n, q;
scanf("%d%d", &n, &q);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
while (q--) {
scanf("%d", &t);
int idx1 = bs1(0, n - 1);
int idx2 = bs2(0, n - 1);
if (a[idx1] == t)
printf("%d %d\n", idx1, idx2);
else
printf("-1 -1\n");
}
return 0;
}
实数域上的二分
例题:数的三次方根
题目描述
给定一个浮点数,求它的三次方根。
输入格式
共一行,包含一个浮点数
输出格式
共一行,包含一个浮点数,表示问题的解,结果保留
输入样例
1000.0
输出样例
10.000000
题目分析
对于题目给定的数据范围,任何一个数的三次方根
需要注意的是,因为浮点数在计算机中的计算具备精度上的误差,所以很有可能最后
所以一般需要设定一个精度
另外需要注意的是,因为浮点数本身不会有取整得情况,每次都会严格将区间分成两半,所以在根据
示例代码
#include <iostream>
using namespace std;
const double eps = 1e-8;
double n;
bool check(double mid) {
return mid * mid * mid <= n;
}
int main() {
cin >> n;
double l = -100, r = 100;
while (r - l > eps) {
double mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
printf("%.6lf\n", l);
return 0;
}
三分法
例题:求单峰函数的极值
题目描述
给定单峰函数的函数式:
输入格式
无
输出格式
共一行,包含一个浮点数,表示问题的解,结果保留6位小数。
输入样例
无
输出样例
无
题目分析
单峰函数的特点是拥有唯一的极值点,在极值点的两侧单调性都严格递增或递减。
以下图所示的单峰函数
- 若
,则一定为下图的两种情况其一。不管是哪种情况,极大值都在 的右边,所以可以更新 。
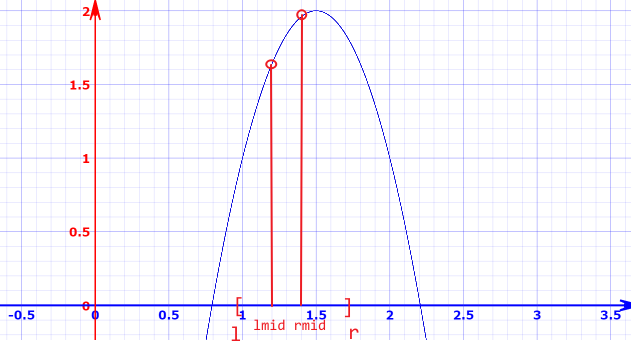
- 同理,若
,则极大值点一定在 的左边,可以更新 。
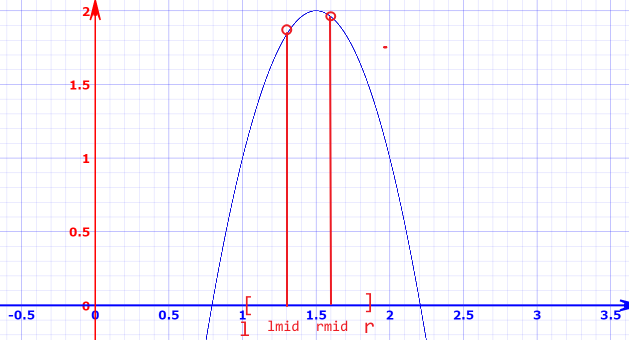
每次都取
示例代码
#include<bits/stdc++.h>
using namespace std;
double eps = 1e-8;
double f(double x) {
return -(2*x-3)*(2*x-3) + 2;
}
bool check(double lmid, double rmid) {
return f(lmid) < f(rmid);
}
int main() {
double l = -100, r = 100; // l和r取极值点两侧即可
while (r - l > eps) {
double lmid = (2*l + r)/3; // [l,r]区间的 1/3 点
double rmid = (l+ 2*r)/3; // [l,r]区间的 2/3 点
if (check(lmid, rmid)) l = lmid;
else r = rmid;
}
printf("%.6lf", f(l));
return 0;
}