排序

排序的定义

排序所起到的作用是把一组“无序”的数据通过一些操作变为“有序”的操作，在算法竞赛中，数据的“有序”可以让我们更快更简单的去达到某些目标。

排序原理

到目前位置，编程中的常见排序算法有十种，详见十大排序算法(暂未更新)，而在本章中，我们重点介绍快速排序和归并排序两种。

快速排序 O(nlog(n))

原理

排序原理：选择一个基准值，将小于基准值的放在左边，大于基准值的放在右边，再递归对左右两个部分进行快速排序，直到排序完成。
实现原理：

  1. 计算基准值 x。
  2. 通过基准值把原数组划分为左右两部分数组，使得左数组都小于 x 而右数组都大于 x。
  3. 递归地对左右数组进行 1,2 两步直到划分的子数组有序。
  4. 当子数组元素只有一个的时候，就认为它是有序的了。——递归边界
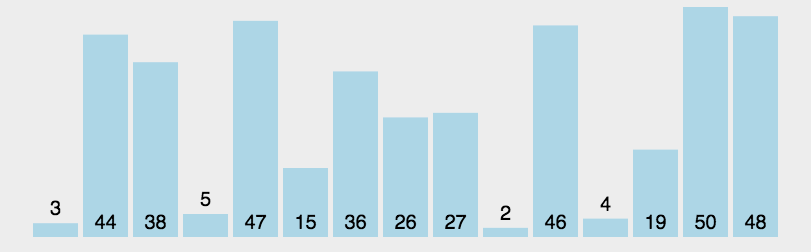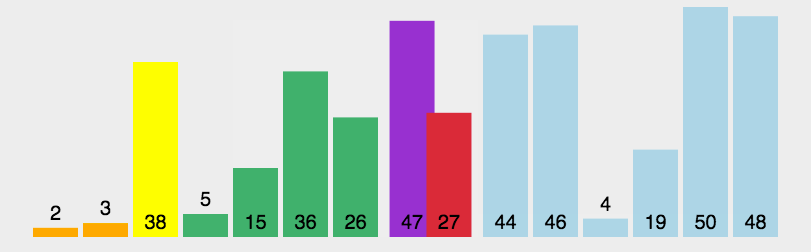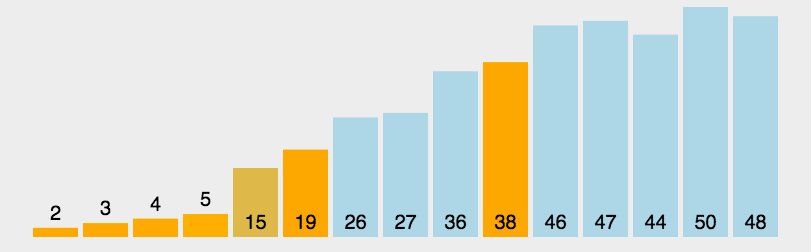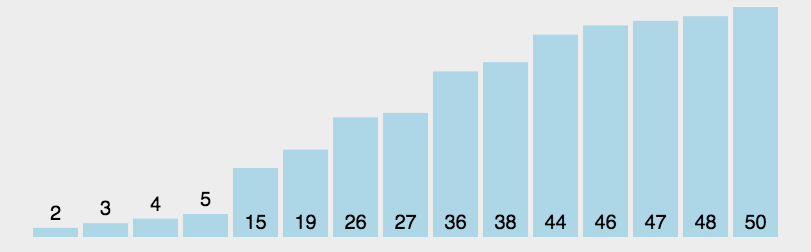
    KutELiN8k6_oZC-9D4cfy.gif

示例代码：

void quick_sort(int l, int r)
{
	if(l == r) return;
	
	int x = f[l + r >> 1], i = l - 1, j = r + 1;
	while(i < j) {
		do i ++; while(f[i] < x);
		do j --; while(f[j] > x);
		if(i < j) swap(f[i], f[j]);
	}
    quick_sort(l, j), quick_sort(j+1, r);
}

快速排序的平均时间复杂度为 O(nlog⁡n)，但当数组基本有序时，会退化为 O(n2)。

例题：第k个数

题目描述

给定一个长度为 n 的整数数列，以及一个整数 k，请求出数列从小到大排序后的第 k 个数。

输入格式

第一行包含两个整数 n 和 k。( 1≤k≤n≤5000000 )
第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整数数列。

输出格式

输出一个整数，表示数列排序后的第 k 个数。

输入样例

 5 3  
 2 4 1 5 3

输出样例

3

示例代码

#include <bits/stdc++.h>
using namespace std;
int k;
void quick_sort(int l, int r, vector<int> &a) {
	if(l >= r) return;
	
	int x = a[l + r >> 1], i = l - 1, j = r + 1;
	while(i < j) {
		do i ++; while(a[i] < x);
		do j --; while(a[j] > x);
		if(i < j) swap(a[i], a[j]);
	}
	if(k <= j) quick_sort(l, j, a);
	else quick_sort(j + 1, r, a);
	
}

void solve() {

	int n;
	cin >> n >> k;
	vector<int> a(n + 10);
	for (int i = 0; i < n; i++)
		cin >> a[i];
	quick_sort(0, n - 1, a);
	cout << a[k - 1];
}

int main() {
	ios_base::sync_with_stdio(0); //数据过大，关闭输入输出流
	cin.tie(0);
	solve();
	return 0;
}

归并排序 O(nlog(n))

排序原理：

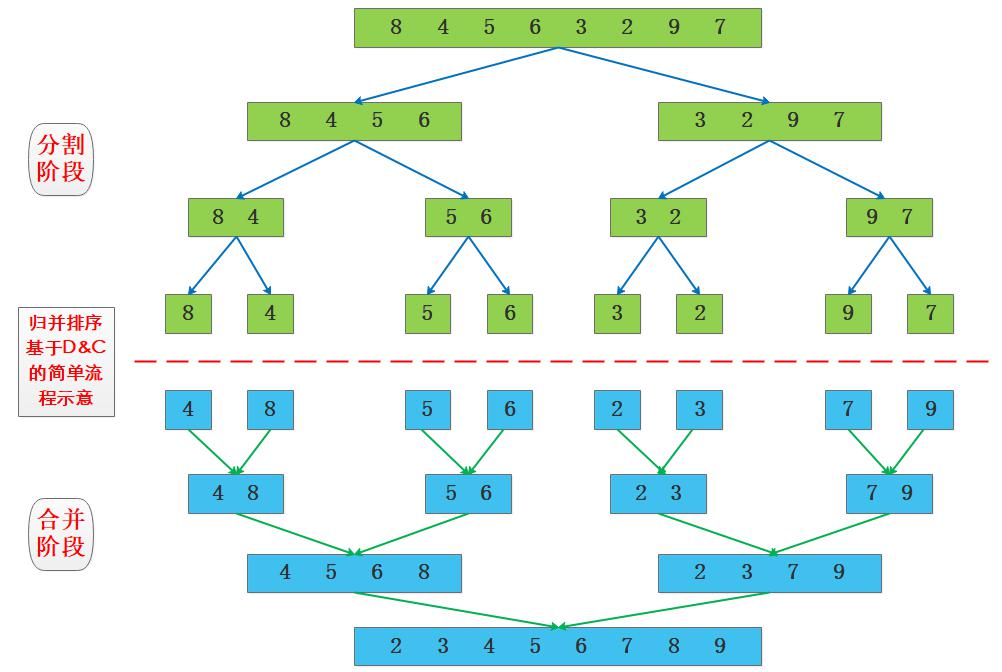
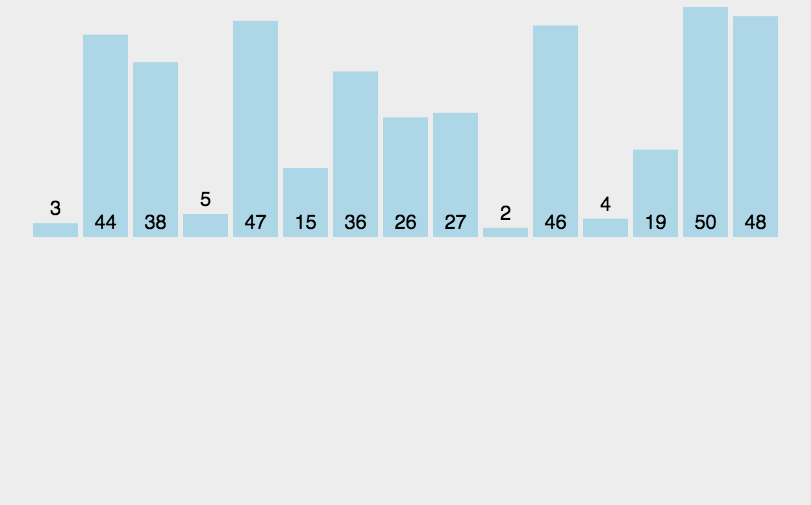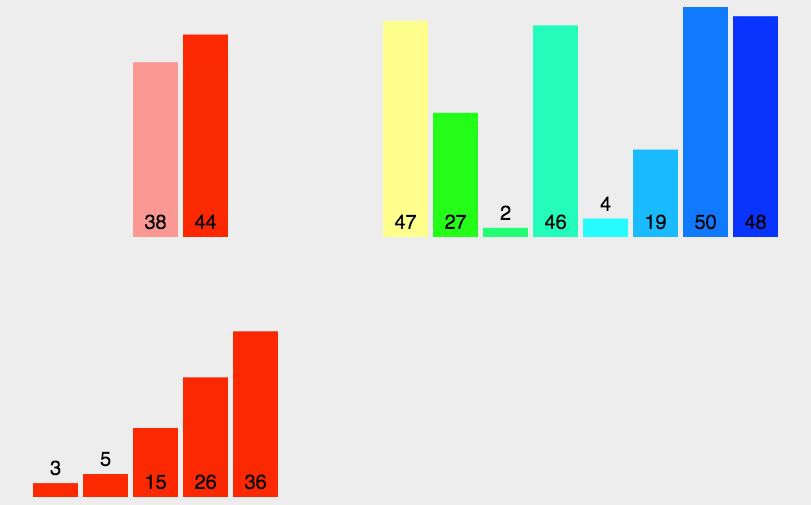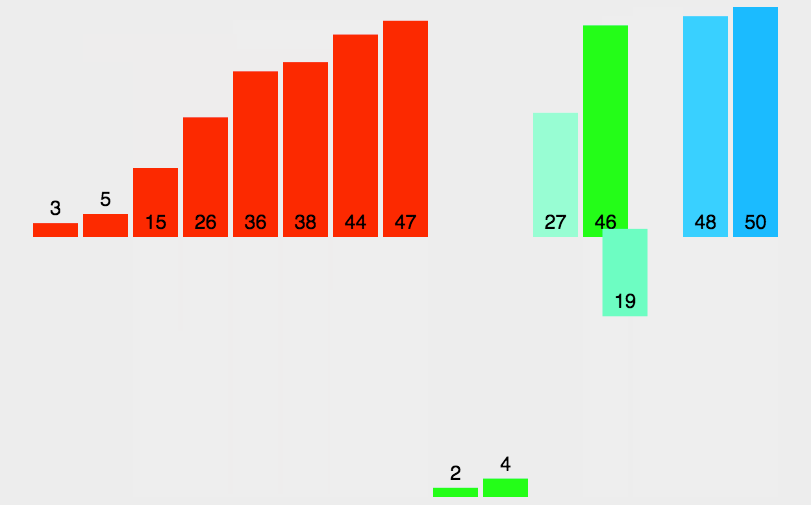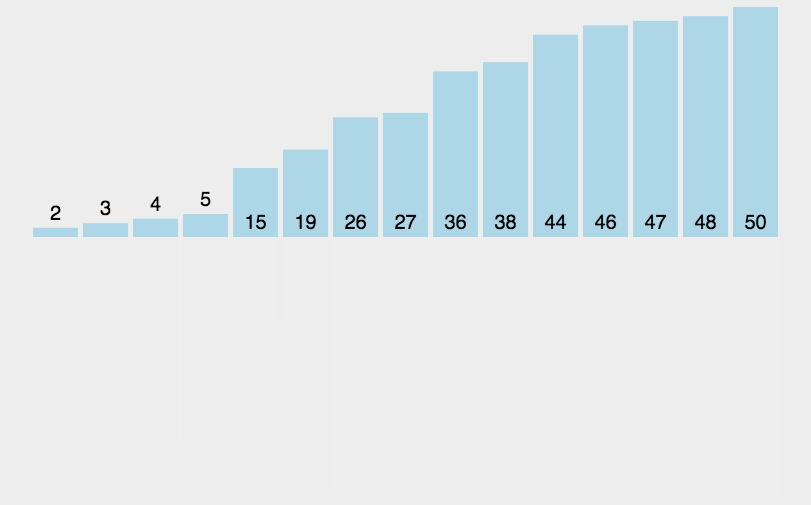
  1. 分解——将待排序数组递归地分成两个子数组，直到每个子数组只有一个元素为止。
  2. 合并——将排好序的子数组按照顺序合并成一个新的有序数组。
  3. 递归调用——重复上述过程，直到所有子数组都被合并成一个有序数组
    XESHK_yQoxQuKAd6HIgki.jpeg

_no9GxsT2N_l7mMD0bSkq.gif

示例代码：

void merge_sort(int q[], int l, int r) {
	if (l >= r) return;  // 只有一个元素
	int mid = (l + r) / 2;
	merge_sort(q, l, mid);
	merge_sort(q, mid+1, r);
	// 归并操作
	int k = 0, i = l, j = mid+1;
	while (i <= mid && j <= r) {
		if (q[i] <= q[j]) {
			temp[k] = q[i];
			k++; i++;
		}
		else {
			temp[k] = q[j];
			k++; j++;
		}
	}
	while (i <= mid) temp[k++] = q[i++];
	while (j <= r) temp[k++] = q[j++];
	for(int i = l, j = 0; i <= r; i++, j++) q[i] = temp[j];
}

例题：求逆序对

题目描述

给定一个序列 a1,a2,…,an，如果存在 ai>aj，那么我们称之为逆序对，求逆序对的数目。 比如：a=[4,2,3,1,5] 逆序对有：(4,2),(4,3),(4,1),(2,1),(3,1) 共 5 对。

输入格式

第一行为n，表示序列长度，第二行 n 个数，表示序列本身。 n≤105，ai≤105。

输出格式

所有逆序对总数。

输入样例

 4   
 3 2 3 2

输出样例

3

题目分析

根据题目可知，逆序对需要满足两个条件：

  1. i<j
  2. ai>aj 思考归并排序合并两个有序数组的过程，对于分解出来的左右数组，左数组的所有元素下标均小于右数组元素下标。当把右数组元素 aj 往辅助数组放时，假设左数组还存在若干元素，对于左数组的任意元素 ai，均满足上面逆序对的两个条件。所以能与 aj 构成逆序对的元素数量即为当前左数组剩余元素个数。

示例代码

#include<iostream>
using namespace std;
const int N = 1e5+10;
int a[N], temp[N];
long long cnt = 0;

void merge_sort(int l, int r) {
	if (l >= r) return;
	int mid = l + r >> 1;
	merge_sort(l, mid);
	merge_sort(mid + 1, r);
	// 归并操作
	int i = l, j = mid + 1, k = 0;
	while (i <= mid && j <= r) {
		if (a[i] <= a[j]) temp[k++] = a[i++];
		else temp[k++] = a[j++], cnt += mid -i + 1; // 当右数组的数往辅助数组放时，可能产生逆序对 
	}
	while (i <= mid) temp[k++] = a[i++];
	while (j <= r) temp[k++] = a[j++];
	
	for (i = l, j = 0; i <= r; i++, j++) a[i] = temp[j];  
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];
    merge_sort(0, n-1);
    cout << count;
    return 0;
}

桶排序 O(n)

排序原理：建立一个桶数组，将每个待排序数据映射到桶数组下标，下标对应的值则表示数据出现的次数。因为桶数组的长度是由数据的大小范围决定的，所以适用于待排序数据范围较小的情况。

void bucket_sort(int q[], int n) {
	for (int i = 0; i < n; i++) // n是数组长度
		temp[q[i]] ++;
	for (int i = 0, j = 0; j < n; i++) // 将桶中的元素按顺序赋值到原始数组 
	{
		while (temp[i] > 0) {
			q[j++] = i;
			temp[i]--;
		}
	}
}

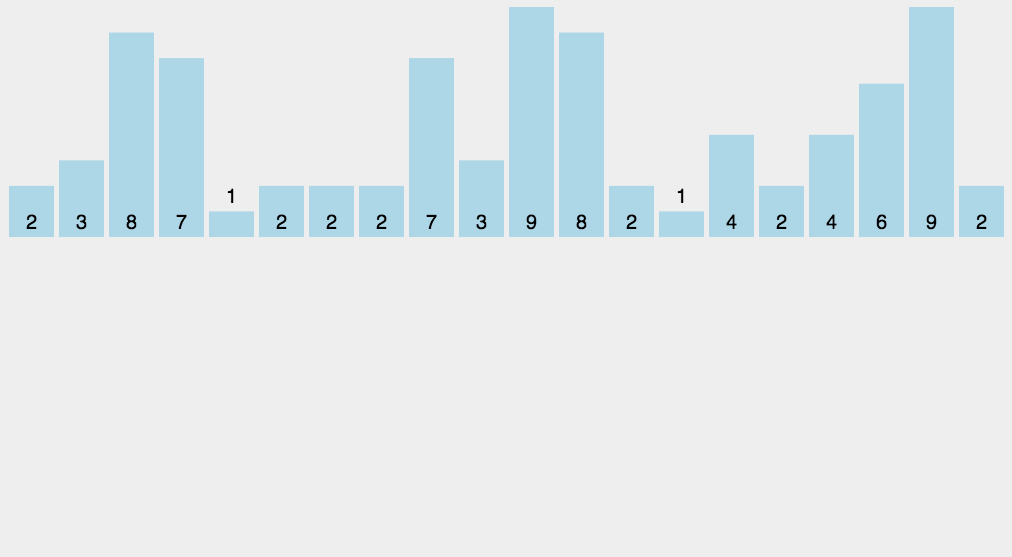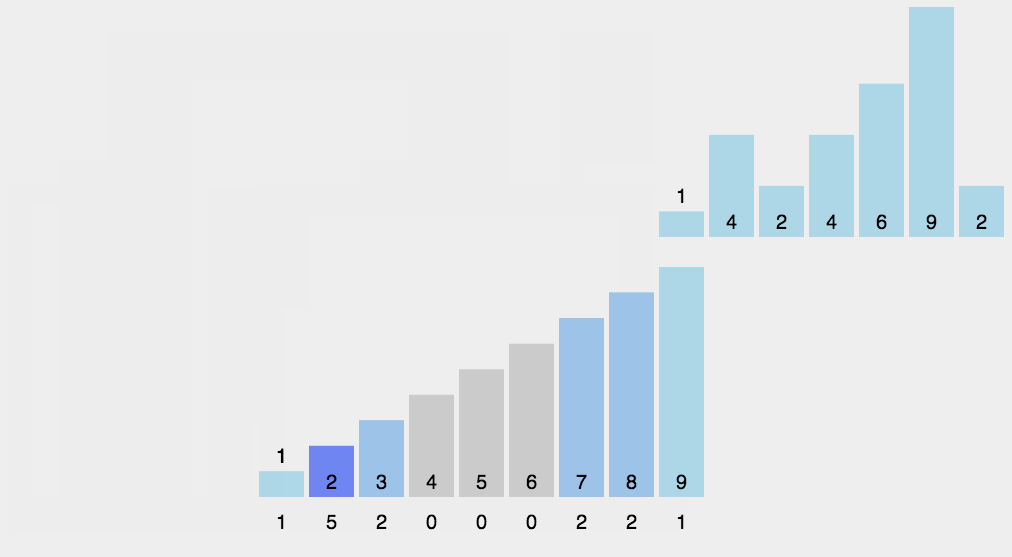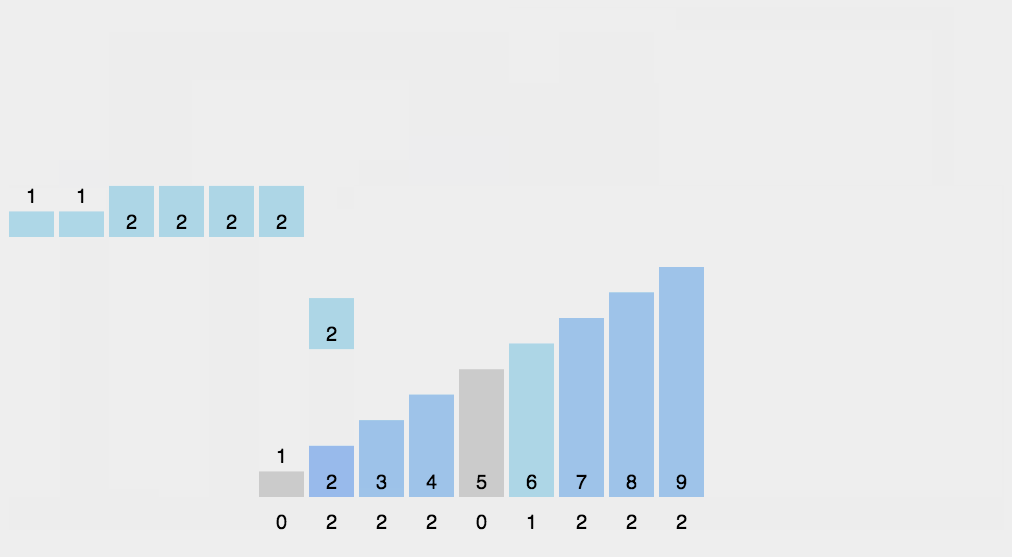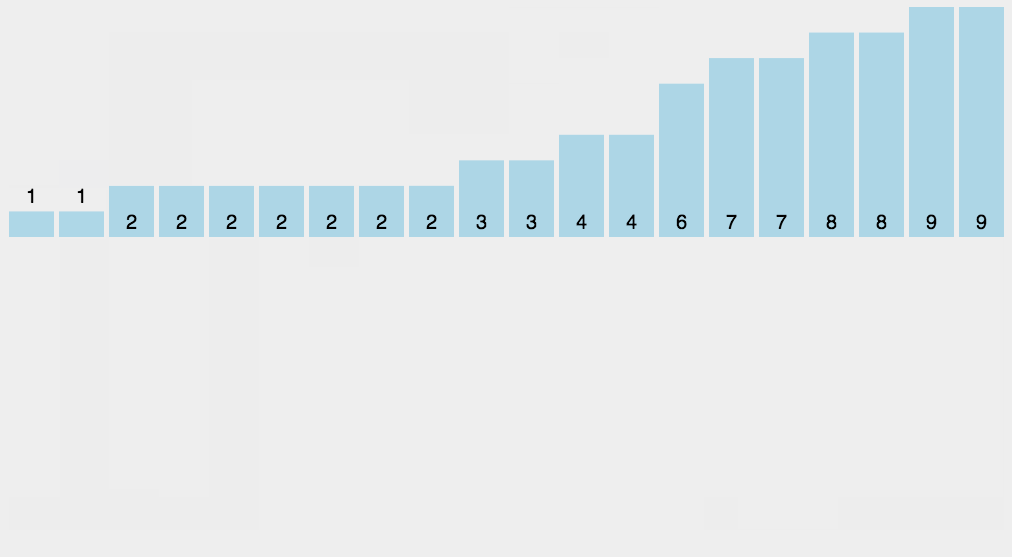
VWZC99-6SRYBXGSNbRi4H.gif

桶排序的常见用法:

//1.排序并去重
for (int i = 0; i < n; i++)
	st[a[i]] = 1;
for (int i = 0; i < N; i++)
	while (st[i]--)
		cout << i << " "; 

//2.排序不去重
for (int i = 0; i < n; i++)
	st[a[i]] ++;
for (int i = 0; i < N; i++)
	while (st[i]--)
		cout << i << " ";

//3.不排序只去重
for (int i = 0; i < n; i++) {
	int x;
	cin >> x;
	if (!st[x])
	{
		cout << x << " ";
		st[x] = 1;
	}
}