前缀和与差分

一维前缀和

来看一道例题：

例题 前缀和

题目描述

输入一个长度为 $n$ 的整数序列。接下来再输入 $m$ 个询问，每个询问输入一对 $l,r$。

对于每个询问，输出原序列中从第 $l$ 个数到第 $r$ 个数的和。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数。

接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$ 表示。

$1\le l\le r\le n$，$1\le n,m\le 100000$，$-1000\le \mathrm{数}\mathrm{列}\mathrm{中}\mathrm{元}\mathrm{素}\mathrm{的}\mathrm{值}\le 1000$

输出格式

共 $m$ 行，每行输出一个询问的结果。

样例输入

6 3
1 3 6 5 4 2
1 3
2 5
3 6

样例输出

10
18
17

题目分析

容易想到如下解法：

for (int i = 1; i <= n; i++) cin >> a[i];
while (q--)
{
    int l, r, sum = 0;
    cin >> l >> r;
    for (int i = l; i <= r; i++) sum += a[i];
    cout << sum << endl;
}

考虑上面算法的时间复杂度，外层循环 $n$ 次，内层循环 $q$ 次，为 $O(n\times q)$，由于 $n,q$ 最大都能取到 ${10}^5$，肯定超时了。 那有没有什么办法可以快速求得 $[l,r]$ 之间的区间和呢？当然有，那就是前缀和数组的妙用了。

前缀和 是指一个数组中，从第一个元素开始，到当前元素为止的所有元素之和。

例如：假设有一个数组 $[1,2,3,4,5]$，我们可以计算它的前缀和数组 $s$ 为 $[1,3,6,10,15]$。

这个前缀和数组的含义是，$s[1]$ 为 $1$，$s[2]$ 为 $1+2=3$，$s[3]$ 为 $1+2+3=6$，以此类推。。。

可以发现，对于数组 $a$，其前缀和数组中的元素：

所以前缀和的构造公式就是：$sum[i]=sum[i-1]+a[i]$。

来看如下例子：

回到我们的问题，我们要求的是给定一段区间 $[l,r]$ 之间的和，那这个前缀和数组有什么用呢，它又如何帮我们求区间和？

到这里可以发现，要求 $a[l]+...+a[r]$ 之间的区间和，只需要构造出 $a$ 的前缀和数组 $s$ 后，用 $s[r]-s[l-1]$ 即可求出，时间复杂度为 $O(1)$。

示例代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n, m, l, r;
int a[N], sum[N];

int main() {
	cin >> n >> m;
	for (int i=1; i<=n; i++) {
		cin >> a[i];
		sum[i] = sum[i-1]+a[i];
	}
	while (m--) {
		cin >> l >> r;
		cout << sum[r]-sum[l-1] << '\n';
	}
	return 0;
}

一维差分

差分为前缀和的逆运算，一般用来对数组某一段区间的值进行快速修改，我们也先来看一道题目：

例题 差分

题目描述

输入一个长度为 $n$ 的整数序列。

接下来输入 $m$ 个操作，每个操作包含三个整数：$l,r,c$。表示将序列 $[l，r]$ 之间的每个数加上 $c$。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数序列。

接下来 $m$ 行，每行包含三个整数 $l,r,c$，表示一个操作。

$1\le n,m\le 100000$，$1\le l\le r\le n$，$-1000\le c\le 1000$，$-1000\le \mathrm{整}\mathrm{数}\mathrm{序}\mathrm{列}\mathrm{中}\mathrm{元}\mathrm{素}\mathrm{的}\mathrm{值}\le 1000$

输出格式

共一行，包含 $n$ 个整数，表示最终序列。

样例输入

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

样例输出

3 4 5 3 4 2

题目分析

这个问题很容易想到暴力解，每次都循环遍历 $[l,r]$ 区间，然后依次加 $c$ 即可，核心代码如下：

int a[100010];
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
while (m--)
{
    int l, r, c;
    cin >> l >> r >> c;
    for (int i = l; i <= r; i++) a[i] += c;
}
for (int i = 1; i <= n; i++) cout << a[i] << " ";

不难看出这个代码的时间复杂度是 $O(m\times n)$ 级别的，如果数据范围较大，代码肯定是超时的。
那么，有没有什么技巧可以 快速对序列中某一连续区间的值进行修改 呢？答案就是 —— 差分！

下面我们先来学习差分数组的概念：
设有 $a，b$ 两个数组，若 $a$ 数组为 $b$ 数组的前缀和数组，我们则称 $b$ 数组为 $a$ 数组的差分数组。差分和前缀和是相反的关系。

根据前面学习的前缀和数组和原数组的关系：
$a[i]=a[i-1]+b[i]$
$b[i]=a[i]-a[i-1]$
即差分数组的第 $i$ 项等于原数组的第 $i$ 项和第 $i-1$ 项的差，对差分数组求前缀和，即得到了原数组。

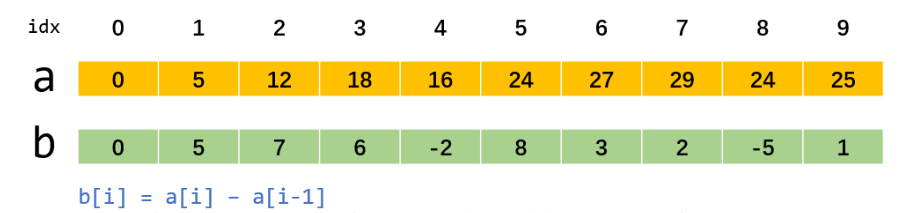
可以尝试一下，如果 差分数组 $b$ 中的某一项的值发生了改变，那么通过前缀和求出来的原数组 $a$ 会发生什么呢？例如上面的 $b[4]$ 如果从 $-2$ 变成了 $0$，即增加了 $2$ 。

那么还原出来的 $a$ 序列就会变成 $[0,5,12,18,18,26,29,31,26,27]$，后面的所有元素都增加了 $2$ ！
那如果此时再让 $b[7]$ 减少 $2$ 呢？即 $b[7]$ 从 $2$ 变成了 $0$，那么再求 $a$ 序列，会得到：

$[0,5,12,18,18,26,29,29,24,25]$，发现了么，现在变成了 区间 $[4,6]$ 之间增加了 $2$，其他的元素保持不变！

那么再往下推导，如果想要 原序列中区间 $[l,r]$ 中的元素都增加 $c$，就把 差分数组中的 $b[l]+c$，$b[r+1]-c$ 即可。

这样每次只需要改变两个元素的值，所以就达到了 快速对序列中某一连续区间的值进行修改 的目的。

总结，利用差分数组来改变原数组中的区间值，操作步骤如下：

• 根据原数组求出差分数组 $b$。
• 要使 $[l,r]$ 区间的值 增加 $c$，就让 $b[l]+c,b[r+1]-c$。
• 求出差分数组 $b$ 的前缀和，即可得到修改后的原数组。

下面来看看如何解决上面的问题，示例代码如下。

示例代码

#include<bits/stdc++.h>
using namespace std;

int n, q, a[100010], b[100010];
int main() {
    cin >> n >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        b[i] = a[i] - a[i - 1]; // 构造a的差分数组b
    }
    while (q--) {
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;   // 操作差分数组b
        b[r+1] -= c;
    }
    for (int i = 1; i <= n; i++) {
        b[i] += b[i-1];
        cout << b[i] << " "; // 对b求前缀和得到修改后的a
    }
    return 0;
}

二维前缀和

二维前缀和的原理和一维前缀和类似，不过求的是一个矩阵内的所有元素的和。

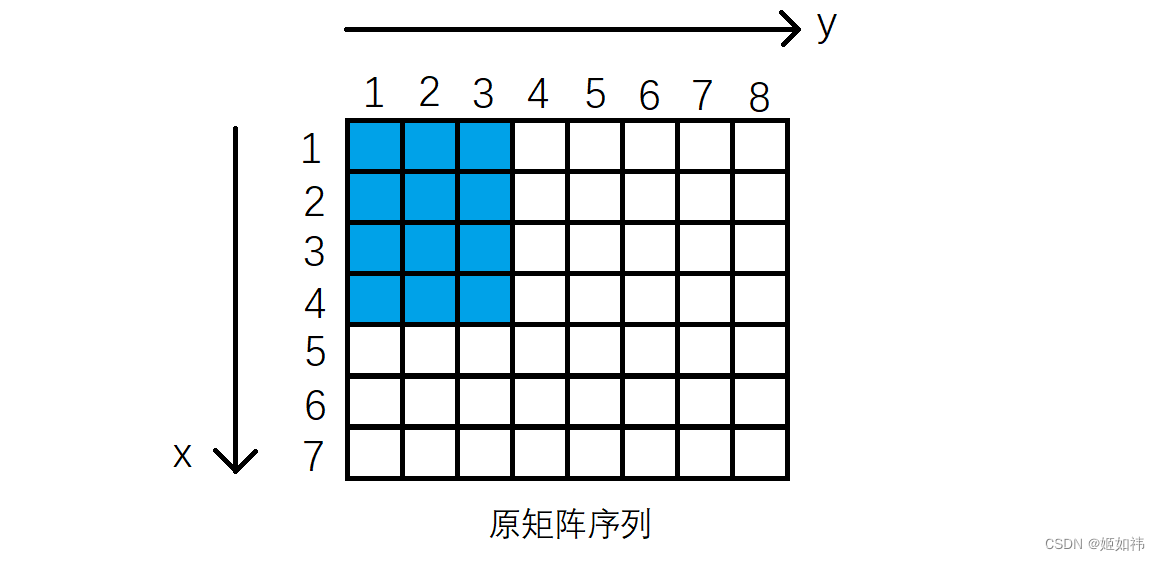
例如上图标蓝的部分，就是从 $(1,1)$ 到 $(4,3)$ 的所有元素的总和，即，对于二维前缀和 $s[i][j]$，表示的是矩阵 $a[1][1]+...+a[i][j]$ 的总和。

那么如何求出二维前缀和呢？对于上面展示的矩阵，如果要求 $s[4][3]$，我们要思考的就是如何求出 蓝色区域中去掉 $a[4][3]$ 后的值。

可以发现，根据容斥原理，其实就是 $s[3][3]+s[4][2]-s[3][2]$，最后再加上 $a[4][3]$ 就可以求出这块的前缀和了。

展开来说，$s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]$，就是二维前缀和的递推公式了。

二维前缀和的作用：求矩阵中某一个小矩阵的元素总和。

思考一下，如果要求 左上角坐标为 $(x1,y1)$，右下角的坐标为 $(x2,y2)$ 的矩阵元素和，如何利用前缀和矩阵来求呢？

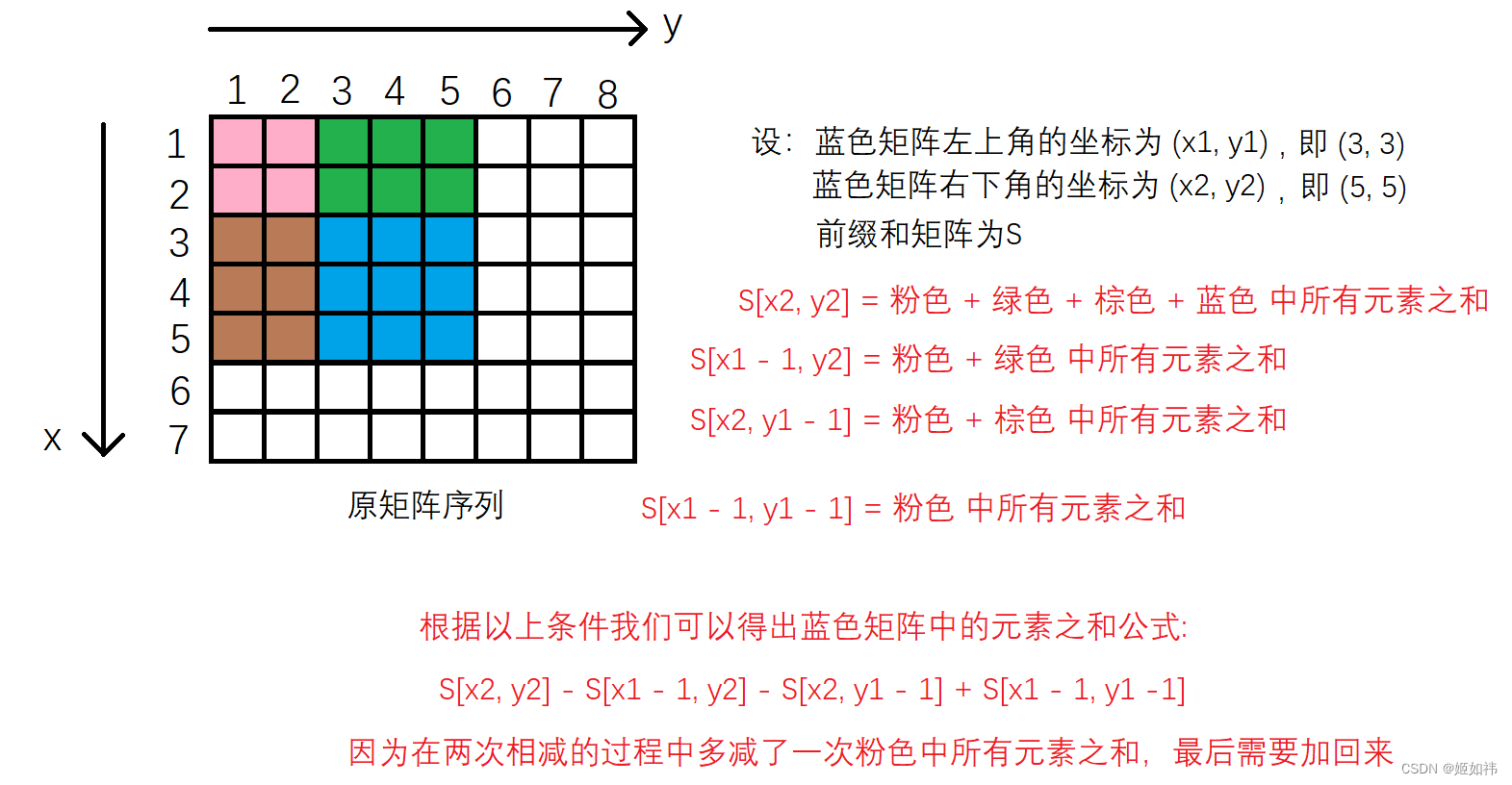
即，求 左上角坐标为 $(x1,y1)$，右下角的坐标为 $(x2,y2)$ 的矩阵元素和，公式为：

$s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]$

例题：子矩阵的和

题目描述

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个询问，每个询问包含四个整数 $x1,y1,x2,y2$，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问，输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 $n，m，q$。

接下来 $n$ 行，每行包含$m$个整数。

接下来 $q$ 行，每行包含四个整数 $x1,y1,x2,y2$，表示一组询问。

$1\le n,m\le 1000,$$1\le q\le 200000,$$1\le x1\le x2\le n,$$1\le y1\le y2\le m,$$-1000\le \mathrm{矩}\mathrm{阵}\mathrm{内}\mathrm{元}\mathrm{素}\mathrm{的}\mathrm{值}\le 1000$

输出格式

共 $q$ 行，每行输出一个询问的结果。

样例输入

3 5 4
1 1 6 7 4
6 10 4 9 9
2 6 7 3 7
1 2 2 4
2 4 3 5
2 2 3 5
1 3 2 4

样例输出

37
28
55
26

题目分析

二维前缀和模板题。

示例代码

#include<iostream>
using namespace std;

int a[1010][1010], s[1010][1010];

int main() {
    int n, m, q;
    cin >> n>> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) // 读入数据并求前缀和
        {
            cin >> a[i][j];
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
        }
    
    while (q--) {  // 求子矩阵的和
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        int ans = s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1];
        cout << ans << endl;
    }
 
    return 0;
}

二维差分

一维差分可以在一个序列中快速修改某个连续区间的值，那二维差分就可以在一个矩阵中 快速修改某一子矩阵的值。

根据一维差分的定义，我们已经得知，差分就是前缀和的逆运算，二维也是相同的概念，如果对于一个 矩阵 $s$，是 矩阵 $a$ 的前缀和矩阵，那么 矩阵 $a$ 是矩阵 $s$ 的差分矩阵。

根据二维前缀和的递推公式：$s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]$

可得，二维差分的递推公式：$a[i][j]=s[i][j]+s[i-1][j-1]-s[i-1][j]-s[i][j-1]$

那么，应该如何对差分矩阵 $a$ 进行操作，使得矩阵 $s$ 中 左上角坐标为 $(x1,y1)$，右下角的坐标为 $(x2,y2)$ 的矩阵元素都增加 $c$ 呢？请看下面的图示：

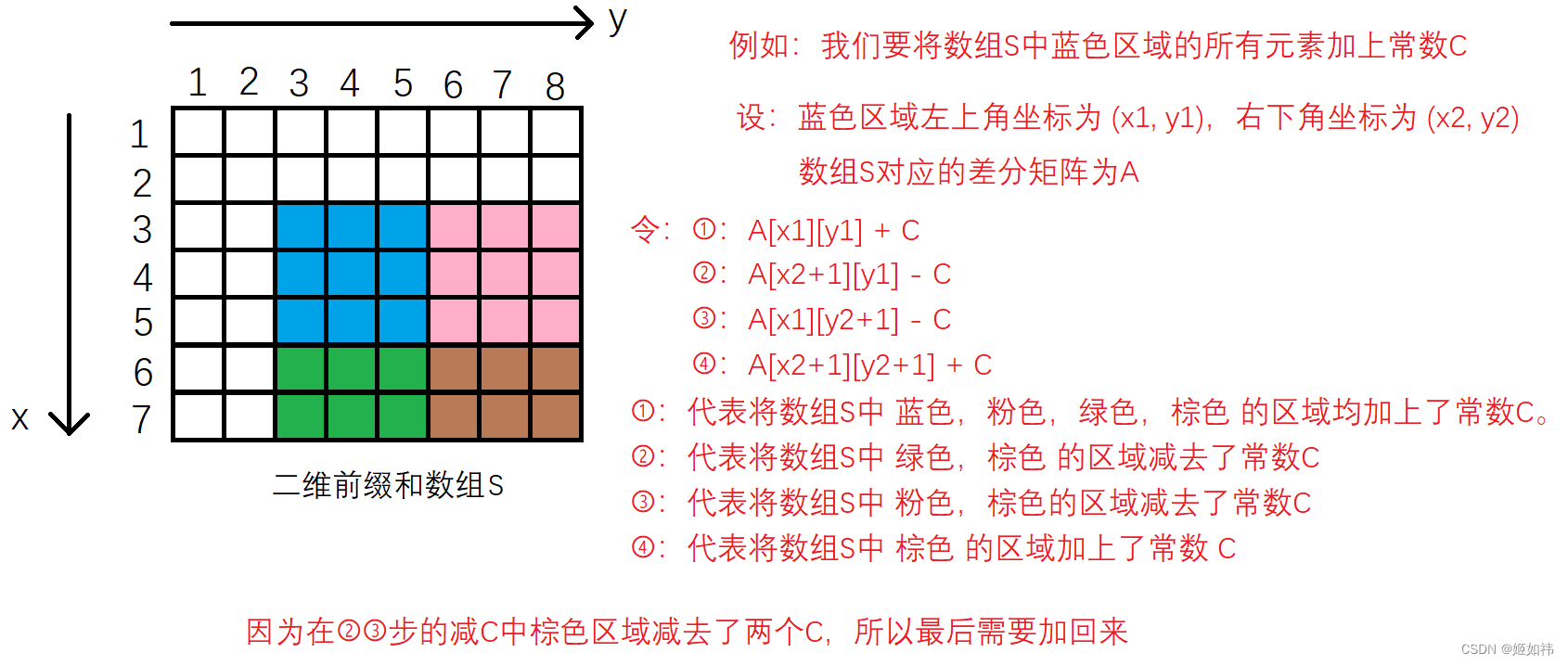
可以发现，如果要将 左上角坐标为 $(x1,y1)$，右下角的坐标为 $(x2,y2)$ 的矩阵元素都增加 $c$ ，就对差分矩阵 $a$ 进行如下操作：

• $a[x1][y1]+c$
• $a[x2+1][y1]-c$
• $a[x1][y2+1]-c$
• $a[x2+1][y2+1]+c$

语句较多，建议定义成函数来完成这个操作。

来看例题。

例题：差分矩阵

题目描述

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个操作，每个操作包含五个整数 $x1,y1,x2,y2,c$。

其中 $(x1,y1)$ 和 $(x2,y2)$ 表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上 $c$。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 $n,m,q$。

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵。

接下来 $q$ 行，每行包含 $5$ 个整数 $x1,y1,x2,y2,c$，表示一个操作。

数据范围：
$1\le n,m\le 1000,$
$1\le q\le 100000,$
$1\le x1\le x2\le n,$
$1\le y1\le y2\le m,$
$-1000\le c\le 1000,$
$-1000\le \mathrm{矩}\mathrm{阵}\mathrm{内}\mathrm{元}\mathrm{素}\mathrm{的}\mathrm{值}\le 1000$

输出格式

共 $n$ 行，每行 $m$ 个整数，表示所有操作进行完毕后的最终矩阵。

样例输入

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

样例输出

2 3 4 1
4 3 4 1
2 2 2 2

题目分析

二维差分模板题。

示例代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    // 使得差分矩阵的指定区域增加 c
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    // 数据读入a
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            cin >> a[i][j];
    
    // 构造a的差分数组b
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            b[i][j] = a[i][j] + a[i-1][j-1] - a[i-1][j] - a[i][j-1];
    // q次操作
    while (q--) {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    // 对b求一次前缀和，得到修改后的a
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + b[i][j];
    // 输出
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=m; j++) {
            cout << b[i][j] << " ";
        }
        cout << endl;
    }
        
    return 0;
}