高精度讲义

前置知识

什么是字符串

详见 05-字符串。

什么是vector

详见 08-STL简单使用#vector。

什么是高精度

高精度算法指用来处理超过计算机固定数据范围的数值计算算法，通常使用字符串或数组等数据结构来存储大数，通过模拟手动计算的过程实现运算。

高精度算法本质是模拟手动列竖式的计算过程，通常会涉及到借位和进位，考虑到数组的性质，中间的插入操作时间复杂度 $O (n)$ ，而末尾的插入为 $O (1)$ ，一般我们把进位存到数组末尾。

高精度加法

以字符串形式读入两个整数 a=12345，b=5839，并将其逆序存储到数组A，B中。
令低位在前，高位在后，如图所示：

A = [5, 4, 3, 2, 1]
B = [9, 3, 8, 5]

计算步骤

① 从低位往高位按位执行加法运算，令 t 为上一位的进位，t 初始为 0。

② 每次循环，当前位数的两个数字以及进位进行相加，并把相加的结果的个位存入结果中，即 c[i] = (t+a[i]+b[i])%10。

③ 计算本次循环的进位，即相加结果的十位，t = c[i] / 10。

④ 循环结束后，如果还有进位，则要加到结果中。

注意：两个大数中，任何一个数没加完，都要继续加。

高精度加法代码模板

vector<int> add(vector<int> A, vector<int> B) {
	vector<int> res;
	int t = 0;
	for (int i = 0; i < A.size() or i < B.size(); i++) {
		if (i < A.size()) t += A[i];
		if (i < B.size()) t += B[i];
		res.push_back(t % 10);
		t /= 10;
	}
	if (t) res.push_back(t);
	return res;
}

高精度减法

存储同高精加。
对于小数减大数情况，会产生负数，为方便处理，我们定义比较函数 cmp，计算时总是让大数减小数，再根据具体情况是否输出负号。

首先思考如何实现比较函数 cmp，数字的比较规则：

数字位数越多的数越大。
位数一样，则从高位到低位逐位比较。

实现的逻辑：a>=b 返回 true，否则 false，代码如下所示：

bool cmp(string a, string b) {
    // a大于等于返回true，否则返回false 
	if (a.size() == b.size()) {
		for (int i = 0; i < a.size(); i++)
			if (a[i] != b[i])
				return a[i] > b[i];
		return true;
	}
	return a.size() > b.size();
}

高精度减法计算步骤

① 从低位往高位计算，令 t 为上一位的借位，t 初始为 0。

② 每次计算时，先把当前位的数字减去 t，即 t = A[i]-t，如果数字 B 中还有数，再减去 B 中的数字。

③ 如果本次计算后数字是小于 0 的，说明要借位，否则说明不用借位。

④ 把本次计算的结果存到结果数组中。

⑤ 重复执行 ②~④ 步

⑥ 计算完成后，去除前导 0，返回结果。

注意：1.借位的问题 2.处理前导0 3.用大数减小数！！

高精度减法代码模板

vector<int> sub(vector<int> A, vector<int> B) {
	vector<int> res;
	int t = 0;
	for (int i = 0; i < A.size(); i++) {
	    t = A[i] - t;
	    if (i < B.size()) t -= B[i];
	    res.push_back((t+10)%10);  // 这段就是如果t大于等于0，结果不变，小于0则计算借位后的结果。
	    if (t < 0) t = 1;  // 记录是否借位。
	    else t = 0;
	}
    while(res.size() > 1 && res.back() == 0) res.pop_back();  // 处理前导0的问题
	return res;
}

高精度乘低精度

数据读入与存储同高精加。

计算步骤

其实计算类似于高精加，而且因为另一个数字是低精度，所以很简单，就是按位相乘，然后处理进位即可。

① 从低往高按位进行乘法，令 t 为上一位的进位，t 初始为 0。

② 计算时，t = t + A[i]*b，那么放入结果中的数字就是 t%10，这一次的进位就是 t/10。

注意：因为乘法的进位可能不止一个，所以循环计算的条件需要加一个 t > 0 ，还有前导 0 问题也需注意。

高精度乘低精度代码模板

vector<int> mul (vector<int> A, int b) {
    vector<int> res;
    int t = 0;
    for(int i = 0; i < A.size() || t; i++)
    {
      	if(i < A.size()) t += A[i] * b;
      	res.push_back(t % 10);
      	t /= 10;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}

高精度除低精度

数据读入与存储同高精加。

计算步骤

模拟除法的过程，除法具备几个特点：

① 是从高位往低位除的。

② 每次除的时候，都会用上一次计算的余数乘10，加上这次的数字再除。

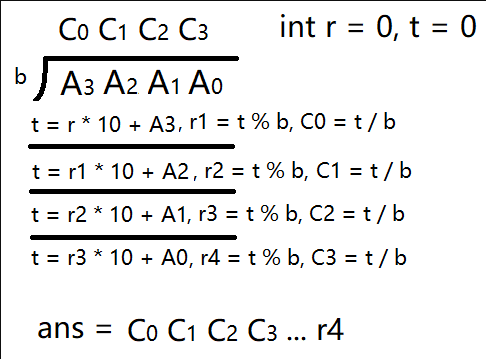
所以代码的实现，也就是根据这两个特点进行即可。

高精度除低精度代码模板

vector<int> div(vector<int> A, int b, int &r) {
    // r用来存储最终计算的余数，是一个引用传参，如果题目需要输出余数则要用。
    vector<int> res;
    int t = 0;
	r = 0;
    for(int i=A.size()-1; i>=0; i--)  // 从高位往低位除
    {
        t = r*10+A[i];
        res.push_back(t/b);
        r = t%b;
    }
    reverse(res.begin(), res.end());  // 反转vector，这样容易来处理前导0问题
    while(res.size()>1 && res.back() == 0) res.pop_back();
    return res;  // 注意，最终返回的结果是逆序的。
}

拓展

高精度乘高精度

可以手算一下一些大数字的乘法，会发现其实是按位相乘，然后最后再加起来计算进位的问题之类的，那么在程序中，按位相乘时，这次计算的结果到底是在哪呢？思考清楚这个问题，高精度乘法也就解决啦。

高精度除高精度

高精度除以高精度用的并不多，结合高精乘和高精减法、高精加可以模拟实现。