枚举讲义

简介

思考如下问题：

给定一个 $n \times m$ 方格的棋盘，求其方格包含多少个正方形、长方形（不包含正方形）。如图所示为 $n = 3, m = 6$ 的棋盘。

比较容易想到，我们可以列出一个矩形的横轴格数和竖轴格数，然后计算出这个矩形在棋盘中有多少个不同的位置，比如在上图棋盘中，横为 $4$ 竖为 $2$ 的棋盘一共有 $6$ 个。

那么如何用编程来实现这个想法呢？关键点在于 列出一个矩形的横轴格数和竖轴格数，最终目标是统计所有方形，所以肯定要 列出所有可能的矩形的横轴格数和竖轴格数，显而易见的是，横轴的格数范围是 $1 - n$ ，竖轴的格数范围是 $1 - m$ ，所以通过以下代码就可以列出所有可能的情况：

for (int i=1; i<=n; i++) {  // i表示横轴格数
	for (int j=1; j<=m; j++) {  // j表示竖轴格数
        ...
    }
}

接下来考虑第二个问题，如何计算横为 $i$ 竖为 $j$ 的方形的数量呢？我们来以方形左上角的点为基准，考虑这个点可以放在哪些位置，横的总长为 $n$ ，方形的横为 $i$ ，那么左上角的位置应该有 $n - i + 1$ 个，下图展示了横为 $6$ ，方形横为 $4$ 时的情况。

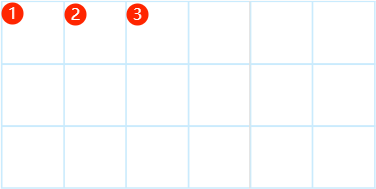
h3BmvmO-77DE60wSiCM7u

同理，竖的总长为 $m$ ，方形的竖为 $j$ 时，左上角的位置应该有 $m - j + 1$ 个，所以左上角位置的总数应该有 $(n - i + 1) \times (m - j + 1)$ 个。

下图展示了 $6 \times 3$ 的棋盘中，方形横为 $4$ 竖为 $1$ 时的情况。

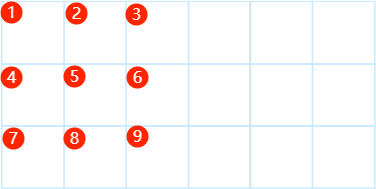
所以可以得出，每次枚举出横为 $i$ 竖为 $j$ 时，方形的数量是 $(n - i + 1) \times (m - j + 1)$ 个，那么把每次计算的结果进行累加，就是答案了。

sum1 = 0, sum2 = 0;  // 正方形和长方形
for (int i=1; i<=n; i++) {  // i表示横轴格数
	for (int j=1; j<=m; j++) {  // j表示竖轴格数
        if (i == j) sum1 += (n-i+1) * (m-j+1);  // 正方形的个数
        else sum2 += (n-i+1) * (m-j+1);  // 长方形的个数
    }
}

上面解决问题的思想，其实就是 枚举法(enumeration method)，又称穷举法，指在一个有穷的、可能的解的集合中，枚举出集合中的每一个元素，用题目给定的检验条件来判断该元素是否符合条件。

用大白话来说，就是把所有可能的情况列出来，然后根据题意判断这种情况是否符合要求。

枚举法常用于解决 “是否存在” 或 “有多少种可能” 等类型的问题，例如上述的统计方形问题。

要点

在设计枚举算法时，通常我们需要考虑以下几个方面：

要枚举哪些东西？是所有的内容都需要枚举吗？
枚举的范围是什么？
枚举的顺序，从小到大还是从大到小？

需要注意的是，很多人在设计枚举算法时思想通常简单粗暴，就是把所有东西全列出来然后逐个判断，这样做虽然减少了思维上的难度，但是伴随而来的就是 Time Limit Execcded，程序超时。

例如前面所讲的统计方形的示例代码，程序的时间复杂度（关于时间复杂度的知识，详见时间复杂度章节）是 $O (n \times m)$ ，当 $n = 10000, m = 10000$ 时，就到达极限了，所以要考虑优化。

优化

在考虑枚举的优化时，一般是找到或者利用一些性质，使得枚举的内容、枚举的范围可以减少。

还是以统计方形这题为例，可以发现正方形的 $i$ 和 $j$ 是完全一样的，那么可以只用一层循环就能算出正方形的个数。

int x = min(n, m);  // 可以思考下这里为什么是取最小值
for (int i=1; i<=x; i++)
	sum1 += (n-i+1) * (m-i+1);

当然，统计长方形的数量还是 $O (n \times m)$ 的时间复杂度。

sum1 = 0;
for (int i=1; i<=n; i++)  // i表示横轴格数
	for (int j=1; j<=m; j++)  // j表示竖轴格数
        if (i != j) sum1 += (n-i+1) * (m-j+1);  // 长方形的个数

从另外一个方向考虑， 矩形的总数 = 长方形的总数 + 正方形的总数，易得 长方形的总数 = 矩形的总数 - 正方形的总数。

那么矩形的总数怎么求呢？其实就是把判断条件给去掉。

sum = 0;
for (int i=1; i<=n; i++)  // i表示横轴格数
	for (int j=1; j<=m; j++)  // j表示竖轴格数
        sum += (n-i+1) * (m-j+1);  // 矩形的总个数

把这个循环展开一层，我们计算的其实是：

for (int i=1; i<=n; i++) {
    sum += (n-i+1)*m + (n-i+1)*(m-1) + ... + (n-i+1)*1;
}

即：(n-i+1)*(m+m-1+m-2+...+1) ，后面这个式子很眼熟，高斯求和公式秒了。

1 + 2 + . . . + n = \frac{n \times (n + 1)}{2}

所以可以得到 (n-i+1) * (m*(m+1)/2) 这个式子，那么循环就变成了：

for (int i=1; i<=n; i++)
    sum += (n-i+1) * (m*(m+1)/2);

相信聪明的你已经发现，(n-i+1) 这块可以用同样的步骤进行优化，最终得到的式子就是：sum = (n*(n+1)/2) * (m*(m+1)/2) 。

那么这样我们的代码流程就可以优化成：

求出矩形的总个数，时间复杂度为 $O (1)$ 。
求出正方形的总个数，时间复杂度为 $O (n)$ 。

所以程序的时间复杂度是 $O (n)$ 。示例代码如下：

#include <bits/stdc++.h>
using namespace std;
long long n, m, sum, cnt; 

int main() {
	cin >> n >> m;
	sum = (n*(n+1)/2) * (m*(m+1)/2);  // 总矩形的个数
	long long x = min(m, n);
	for (int i=1; i<=x; i++) {
		cnt += (n-i+1)*(m-i+1);  // 边长为i的正方形的个数 
	} 
	cout << cnt << " " << sum-cnt;
	return 0;
}

回看上面的优化过程，其实我们就是利用了：

长方形的总数 = 矩形的总数 - 正方形的总数
正方形长宽相等，只需要一层循环
矩形的总数可以利用求和公式直接算出来

这些性质，来实现了时间复杂度为 $O (n)$ 级别的算法，在所有枚举的题目中，都可以用类似的思想去考虑优化。

再优化

爱钻研的你或许还有疑问，既然矩形能够通过公式直接进行计算，那么正方形的数量呢？如果正方形的数量也能用公式算，那么这个算法的时间复杂度将达到完美的 $O (1)$ 级别。

来观察下循环中求和的本质：

cnt = n*m + (n-1)*(m-1) + (n-2)*(m-2) + ... + (n-x+1)*(m-x+1)
    = n*m + (n-1)*(m-1) + (n-2)*(m-2) + ... + (n-(x-1))*(m-(x-1))
    = n*m + n*m-n-m+1 + n*m-2*n-2*m+4 + ... + n*m-(x-1)*n-(x-1)*m+(x-1)*(x-1)
    = x*n*m - n*(1+2+..+(x-1)) - m*(1+2+..+(x-1)) + (1*1+2*2+..+(x-1)*(x-1))

很容易可以发现，n*(1+2+..+(x-1)) 和 m*(1+2+..+(x-1)) 都可以用高斯求和公式来计算，得到：

n*(x-1)*x/2 + m*(x-1)*x/2

即：

(n+m)*(x-1)*x/2

而最后的 (1*1+2*2+..+(x-1)*(x-1))，则是经典的平方和公式。

1 \times 1 + 2 \times 2 + . . . + n \times n = \frac{n \times (n + 1) \times (2 n + 1)}{6}

所以这个式子可以用 (x-1)*x*(2*x-1)/6 计算得出，最终的公式为：

cnt = x*n*m - n*(x-1)*x/2 - m*(x-1)*x/2 + (x-1)*x*(2*x-1)/6;

那么最终代码就变成了：

#include <bits/stdc++.h>
using namespace std;
long long n, m, sum, cnt; 

int main() {
	cin >> n >> m;
	sum = n*(n+1) * m*(m+1)/4;  // 总矩形的个数
	long long x = min(n, m);
	long long cnt = x*n*m - n*(x-1)*x/2 - m*(x-1)*x/2 + (x-1)*x*(2*x-1)/6;
	cout << cnt << " " << sum-cnt;
	return 0;
}

总结

枚举算法是算法中最基础的一种，也是我们日常生活中经常会使用的方法，再进行程序设计时，最重要的点就是找到要枚举的东西、枚举的范围、枚举的顺序。

其次，在设计完枚举算法后，一定要去考虑代码能否去进行优化，多留意题目中给出的条件，这些条件既是限制，也是我们减少枚举内容的关键点。