离散化与区间合并

离散化

离散化的概念

离散化本质上可以看成是一种 哈希，其保证数据在哈希以后仍然保持原来的全/偏序关系。

通俗地讲就是当有些数据因为本身很大或者类型不支持，自身无法作为数组的下标来方便地处理，而影响最终结果的只有元素之间的相对大小关系时，我们可以将原来的数据按照从大到小编号来处理问题，即离散化。

例题：区间和

题目描述

假定有一个无限长的数轴，数轴上每个坐标上的数都是 $0$。

现在，我们首先进行 $n$ 次操作，每次操作将某一位置 $x$ 上的数加 $c$。

接下来，进行 $m$ 次询问，每个询问包含两个整数 $l$ 和 $r$，你需要求出在区间 $[l,r]$ 之间的所有数的和。

输入格式

第一行包含两个整数 $n$ 和 $m$。

接下来 $n$ 行，每行包含两个整数 $x$ 和 $c$。

再接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$。

$-{10}^9\le x\le {10}^9,1\le n,m\le {10}^5,-{10}^9\le l\le r\le {10}^9,-10000\le c\le 10000$

输出格式

共 $m$ 行，每行输出一个询问中所求的区间内数字和。

输入样例

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例

8
0
5

题目分析

对于该题，很容易想到可以用前缀和来处理连续区间的和，但是若将输入的 $x$ 直接作为数组下标实在太大了($-{10}^9\sim {10}^9$ 肯定没法开这么大的数组，即使能开也没法循环一遍求前缀和。)

所以我们就需要考虑，能否不直接把 $x$ 作为数组下标，而是通过一些手段，将它们映射到相邻的数组空间中，如下图所示：

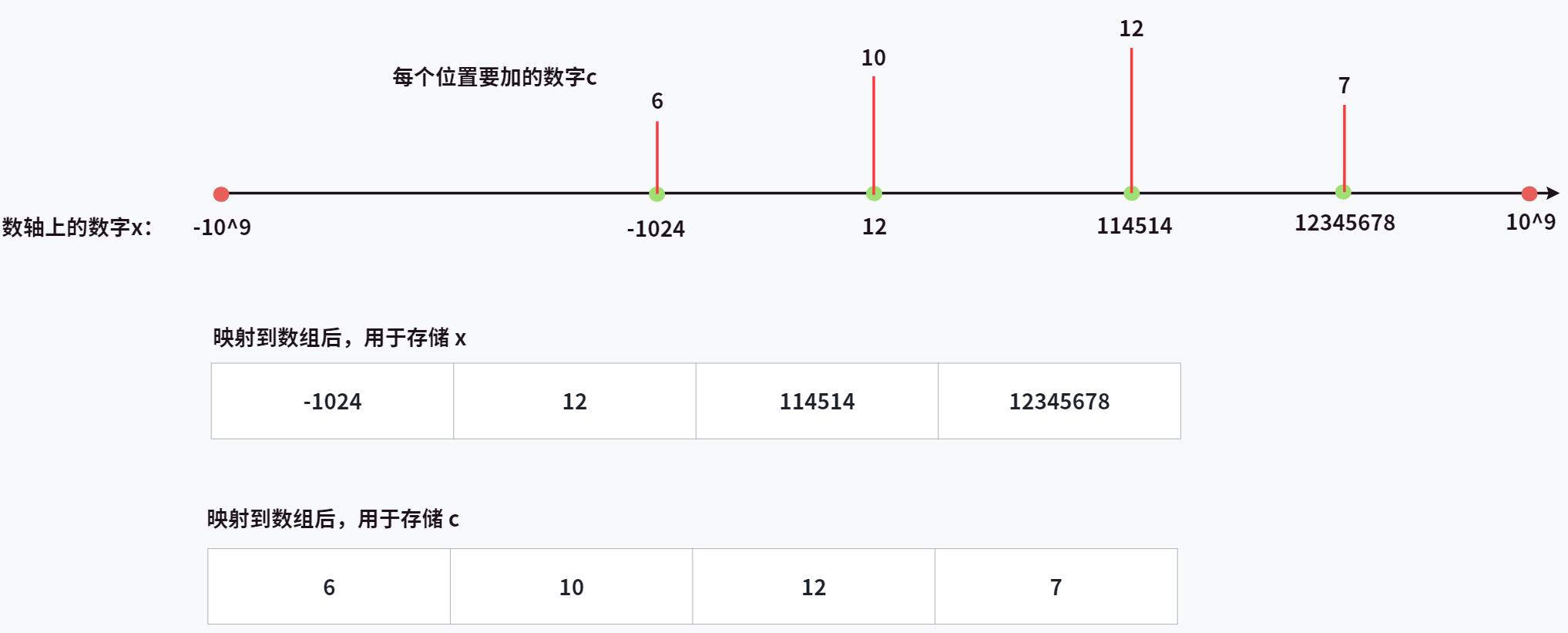
试想，数字的数量最多是 ${10}^5$，那么实现如上操作后，数组完全可以存的下，并且循环遍历也不会有超时的问题。

像本题的区间和问题，那就可以对 存 $c$ 的数组求前缀和；而查询区间和时，要注意的是输入的 $l$ 和 $r$ 也是数轴上的数字，而不是映射后的数组的下标，所以还需要再存 $x$ 的数组中查找 $l$ 和 $r$ 的下标。怎么查比较快呢？

可以发现，存 $x$ 的数组是有序的，那么答案只有一个了，那就是——二分查找！

理论可行，关键就在于如何把所有的 $x$ 按顺序离散化到数组上。

让我们一步一步来，首先先抛开要加的 $c$ 不管，先解决如何把所有的 $x$ 存下来，很明显就是把每次输入的 $x$ 放到数组中，然后进行排序即可。

不过要注意的是，题目输入的 $x$ 可能会有重复，而我们通过映射后的 $x$ 对应的下标应该只会有一个，然后把所有的 $c$ 到加到同一个下标里，这样才好操作，所以不仅需要排序，还需要去重！
另外，为了之后查找 $l$ 和 $r$ 更方便的定位其区间，把 $l$ 和 $r$ 也加入到映射的数组中是比较好的选择，这样就可以得到一段代码：

vector<int> alls;

for (int i=1; i<=n; i++) {
	cin >> x >> c;
	alls.push_back(x);
}
for (int i=1; i<=m; i++) {
	cin >> l >> r;
	alls.push_back(l);
	alls.push_back(r);
}
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());

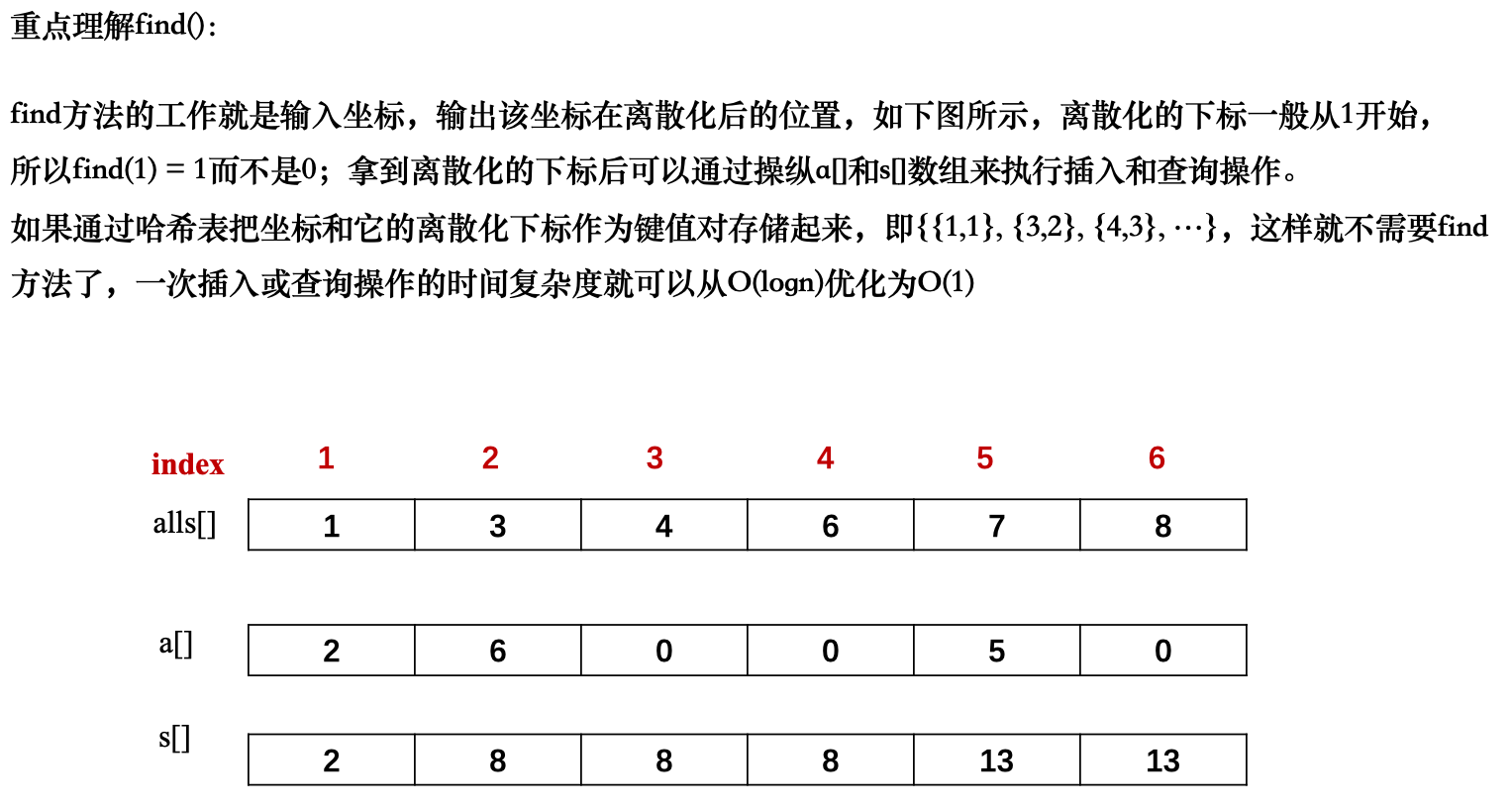
接下来处理第二个问题，怎么把 $c$ 加到对应的位置上呢？

要知道一点，到这里 alls 数组已经进行离散化了，是一个有序且不重复的数组，每个数字 $x$ 在上面都有其对应的下标，而且可以使用二分查找来找到这个下标。

所以，解决方案就是：通过二分查找找到这个 $x$ 的下标，然后让这个下标再加上 $c$。

int a[300005];
vector<pair<int,int>> add;

int find(int x) {  // 二分查找第一个大于等于x的位置
	int l = 0, r = alls.size()-1, mid;
	while (l < r) {
		mid = l + r >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid+1;
	}
	return r+1;  // 加1是为了让离散化的下标从1开始，方便求前缀和。
}

for (int i=1; i<=n; i++) {
	cin >> x >> c;
	add.push_back({x, c});
	// 这里省略上面那段处理 alls 数组的代码。
}

for (auto item : add) {
    int x = find(item.first);  // 查找 x 离散化后的下标
    a[x] += item.second;  // 对应下标上加上 c
}

最后的查找也很简单，先对 a 数组求出前缀和后，只需要在输入时把 $l$ 和 $r$ 先存下来，等离散化处理完后，再遍历，每次用二分找到 $l$ 和 $r$ 的下标，再用前缀和数组来求区间和即可。

示例代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
typedef pair<int, int> PII;
const int N = 300010;

int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x) {
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i ++ ) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        alls.push_back(x);
    }

    for (int i = 0; i < m; i ++ ) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});
        alls.push_back(l);
        alls.push_back(r);
    }

    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 处理插入
    for (auto item : add) {
        int x = find(item.first);
        a[x] += item.second;
    }

    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    // 处理询问
    for (auto item : query) {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }
    return 0;
}

区间合并

基本概念

所谓区间合并，就是对给定的n个区间，将有交集（包含端点）的若干个小区间合并为一个大区间。

例题：区间合并

题目描述

给定 $n$ 个区间 $[l_i,r_i]$，要求合并所有有交集的区间。注意如果在端点处相交，也算有交集。输出合并完成后的区间个数。例如：$[1,3]$ 和 $[2,6]$ 可以合并为一个区间 $[1,6]$。

输入格式

第一行包含整数 $n$。

接下来 $n$ 行，每行包含两个整数 $l$ 和 $r$。

数据范围：
$1\le n\le 100000$；$-{10}^9\le l_i\le r_i\le {10}^9$

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

输入样例

5
1 2
2 4
5 6
7 8
7 9

输出样例

3

题目分析

从两个区间的位置关系出发进行考虑，假设已经按区间的左端点进行排序，有如下三种位置关系：

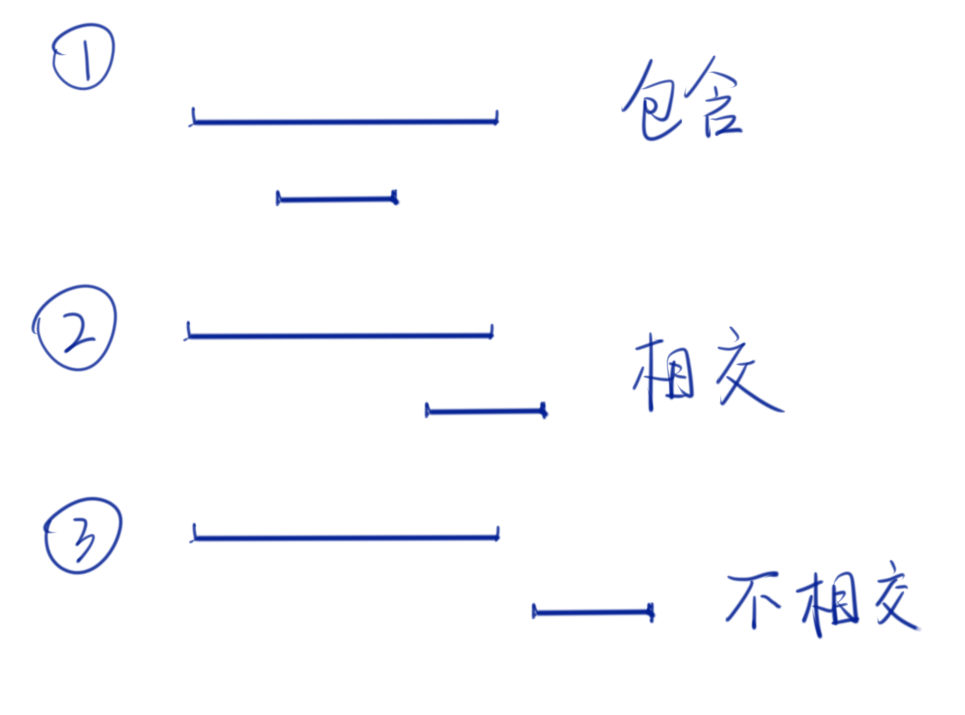
令当前区间的左端点为 st，右端点为 ed，假设待合并区间为 $i$，其左右端点分别为 i.st、i.ed 。

合并思路：贪心！

情况①：当前区间包含待合并区间时，st, ed => st, ed，还是原区间。

情况②：当前区间与待合并区间相交时，st, ed => st, i.ed，拓展了右区间。

情况③：当前区间与待合并区间不相交时，st, ed => i.st, i.ed，原区间已经是合并完成的独立区间，从下一个新区间重新合并下一个区间。

示例代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

void merge(vector<PII> &segs) // 合并两个区间 
{
    vector<PII> res;
    sort(segs.begin(), segs.end()); // pair默认按左端点排序 

    int st = -2e9, ed = -2e9; // 初始化起始断点-∞ 
    for (auto seg : segs) 
        if (ed < seg.first) // 情况3不相交 
        {
        	// 初始-∞端点要跳过 
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second); // 情况1，2相交，取右端点较大值 
	// n=0时特判、最后一个区间压入 
    if (st != -2e9) res.push_back({st, ed});
    segs = res;
}

int main() {
    int n;
    scanf("%d", &n);
    vector<PII> segs;
    
    for (int i = 0; i < n; i ++ ) {
        int l, r;
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }
    
    merge(segs); // 传引用参数 
    cout << segs.size() << endl;
    return 0;
}