进制转换
首先,常见的进制有:
- 十进制,逢十进一,数位上会出现的数字有
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - 二进制,逢二进一,数位上会出现的数字有
0, 1 - 八进制,逢八进一,数位上会出现的数字有
0, 1, 2, 3, 4, 5, 6, 7 - 十六进制,逢十六进一,数位上会出现的数字有
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F,其中A代表10,B代表11,以此类推。
其他进制类似,总之如果是 X 进制,那么就是逢 X 进一,数位上会出现的数字范围是 0~X-1。
进制间的转换
X 进制 转 十进制
转换分为整数部分和小数部分,对于这个转换,我们要理解数位的概念,以十进制为例,什么叫十位、什么叫百位呢?这个位上的数字又代表什么呢?例如十进制数字 327,百位上的数字是 3,意味着这个数字有 3 个 100;十位上的数字是 2,意味着这个数字有 2 个 10;同理,个位为 7 意味着这个数字有 7 个 1。
而 4327 为例,如下图所示:
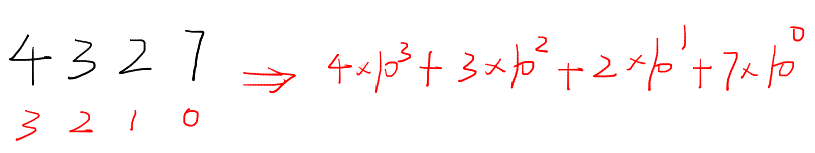
这个算式便组合得到了 4327 这个十进制数字。
那么同样的道理,如果是 八进制 的数字 4327,它的每个数位代表着什么呢?显然,
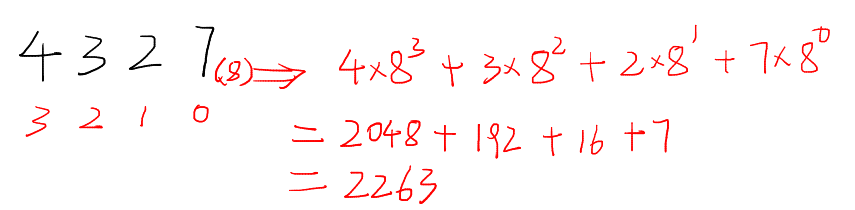
其他进制也是同样的道理。
总结一下,如果有 X 进制的数字要转十进制,那么从后往前依次标号 0,1,2,3...,分别计算 数位上的数字 与 X 的对应次幂,再计算总和即可。
这里再演示下二进制和十六进制转十进制的计算吧。
二进制数 101011
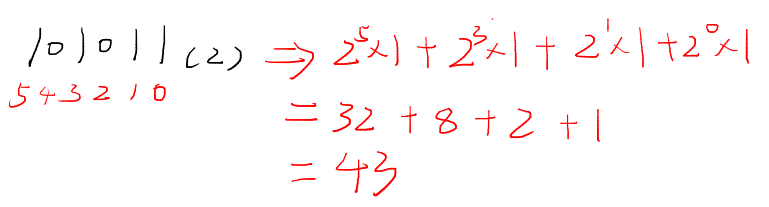
十六进制数 20C,C 代表 12。
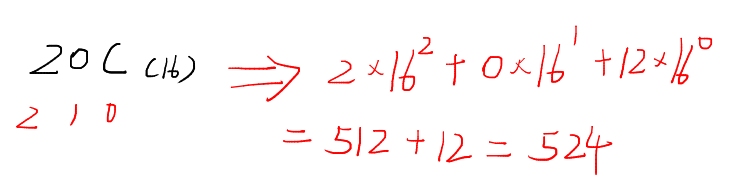
这便是 X 进制转十进制的整数部分了,那如果数字带小数怎么办?
也很简单,同样标号,小数点往后的数字,依次标 -1, -2, -3...,其对应的就是
另,
我们直接来算一个二进制的例子吧。
二进制数 1010.101
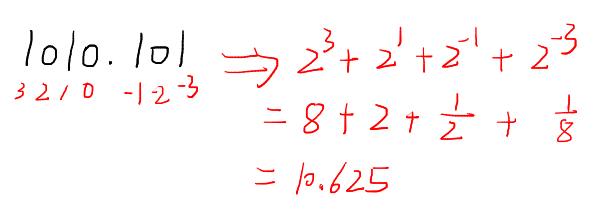
其他进制也是类似的道理,就不多赘述啦!
试着算一算它们的十进制数:
二进制数 11010.011,八进制数 127.4,十六进制数 4F.4
十进制转 X 进制
整数部分,利用除 X 取余法,不断去除以 X,并记录计算出来的余数,直到数字除到 0 为止,最后把计算的余数逆序输出即可。
例如数字 29 转 二进制,计算过程如下图:
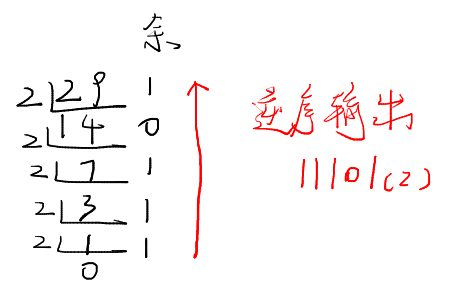
剩下的其他进制也是类似的道理,转八进制就除 8,转十六进制就除 16。
小数部分,利用乘 X 取整法,不断让小数部分乘以 X,并取出计算结果的整数部分,这样就算出了一位,然后小数部分继续下一次计算,不断重复这个过程直到小数部分为 0 或者精度满足了题目的要求为止。
以数字 29.625 转二进制 为例,整数部分计算和前面一样,这里把小数 0.375 拿出来单独进行转换,最终转换出来是 0.011,结合前面的整数部分,就是 11101.011,注意这里取出来的整数是顺序输出的。

其他进制也是同理,就把 乘的 2 换成对应进制即可。
原码补码反码
原码、反码和补码是计算机中表示整数的一种编码方式,主要用于处理带符号数(正数和负数)的表示和运算。 设计原反补码的原因,是因为用补码表示数字可以将减法转换为加法处理,简化硬件设计。计算机中表示和计算整数都是以补码形式进行的。
我们将原反补码统称为机械码,机械码由 符号位 和 数据位 组成,其中符号位只占一位,且通常是最高位,其余为数据位。例如,十六位的机械码,结构为:[ 一位符号位 ][ 十五位数据位 ]。所以为什么 int 类型作为 32 位的二进制存储数据的范围是 -2^31~2^31-1 呢?因为最高位用来做符号位了。
原码计算
先不管符号,把数值转为二进制填入数据位;如果是负数,符号位为 1,否则符号位为 1。
例如,计算 13 的八位原码,先转二进制得 1101,符号位为 0,所以其八位原码为 0000 1101。
如果是 -13 呢?还是把 13 转二进制得 1101,符号位为 1,所以其八位原码为 1000 1101。
反码计算
非负数的原码、反码、补码是一样的。
还是以 13 和 -13 为例,那么 13 的反码就是 0000 1101。
而负数的反码是在原码的基础上,符号位不变,其他位按位取反。
所以,-13 的反码是 1111 0010。
补码计算
非负数的原码、反码、补码是一样的。
还是以 13 和 -13 为例,那么 13 的补码就是 0000 1101。
而负数的补码是在反码的基础上,最后一位加上 1,并处理进位的相关事情。
所以,-13 的补码是 1111 0011。
总结
正数的原反补码都一样。
负数,反码是在原码的基础之上,符号位不变,其他位取反;补码是在反码的基础上加 1。
位运算
位运算的符号一共六个:
&:按位与,两个二进制数尾对齐按位计算,两位都为 1 结果才为 1,例如 1101 & 1010 = 1000
|:按位或,两个二进制数尾对齐按位计算,两位只要由一位是 1 结果就是 1,例如 1101 | 1010 = 1111
~:按位取反,一个二进制数的每一位都取反,例如 ~1010 = 0101。
^:按位异或,两个二进制数尾对齐按位计算,相同为 0,不同为 1。例如 1101 ^ 1010 = 0111
<<:左移指定位数,后面补零,例如 1101 << 2 = 110100,每左移一位相当于实际值乘以 2。
>>:右移指定位数,后面的消掉,例如 1101 >> 2 = 11,每右移一位相当于实际值除以 2。
需要注意的是,数值在计算机中都是以补码形式存储的,在进行位运算时,需要把实际数值转为对应补码,并且除左移右移外,符号位也会参与进位运算中。
例如计算 -2 | 1 的结果,先把两个数字转为补码,这里以 8 位补码为例(实际 int 类型是 32 位,但此处数据较小就用八位代替了):
-2 的八位补码是 1111 1110,1 的八位补码是 0000 0001,两者进行或运算的结果为 1111 1111,这个结果也是补码!!最后转回实际数字得结果是 -1。
再比如计算 ~1,1的八位补码是 0000 0001,按位取反得 1111 1110,注意结果是补码,转回实际数字得结果是 -2。
再再比如计算 3 ^ -2,3的八位补码是 0000 0011,-2 的八位补码是 1111 1110,异或得 1111 1101,转为原码就是 1000 0011,即 -3。
常用位运算技巧
x & 1 可以得到 x 的最低位是 1 还是 0,也可以用来判断奇偶。
x & ~(1 << n) 可以把 x 从后往前数第 n+1 位设为 0。
x | (1 << n) 可以把 x 从后往前数第 n+1 位设为 1。
x & (x-1) 可以把 x 的最低位的 1 设为 0。
x & (-x) 取得 x 最低位的 1 以及其对应的值,例如 12 & (-12),12 的二进制是 1100,那么这个算式得到的就是 100,即 4。
另,GESP 里喜欢考的一个 a = a^b; b = a^b; a = a^b,作用是交换 a,b 的值。